Law of Constant Returns (Explained With Diagram)

Statement of the Law:

The law of constant returns is said to operate when the return remains the same as the business is expanded or contracted.

Every additional investment of labour and capital yields the same return as before.

Or in other words, whatever the scale of production, the cost of the product per un remains the same.

We have said before that, in certain cases, and when the business moves towards the optimum, the returns increase, and when it goes beyond the optimum, the returns decrease. But if, after having reached the optimum point, the industry is stabilized at that level of output, the returns, continue to be the same; and they are said to be constant.

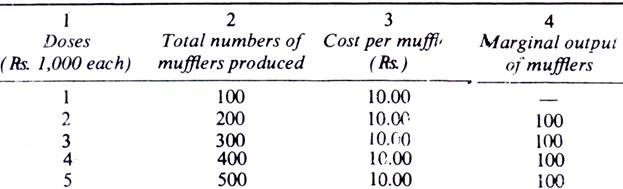
The following table illustrates the law of constant returns

A. muffler manufacturer successively invests doses of Rs. 1,000 each in his business which progresses as follows:

When he invests Rs. 1,000, the number of mufflers produced is 100, and when he spends Rs. 2,000, the number of mufflers produced ,s also doubled, i.e., 200 (column 2). The return is, therefore, proportionate. The cost of production per muffler remains the same, i.e., Rs. 10, whatever the scale of production (column 3). The marginal output remains constant, i.e., 100 (column 4). Every extra investment of Rs. 1,000 yields an additional output of 100 mufflers.

Diagrammatic Representation:

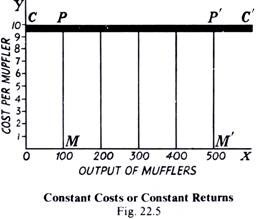
The law of constant returns can be repre­sented in a diagram (Fig. 22.5) thus:

Along OX are measured the successive investments of Rs. 1,000 each, and along OY the marginal or additional output in hundreds of mufflers. The cost is Rs. 10 per muffler in each case, whether 100 or 500 mufflers are produced. This is shown by the line CC running parallel to OX.

Operation If the Law of Constant Returns:

We have already pointed out that in an industry where nature’s influence is dominant, e.g., agriculture, diminishing returns set in quickly, and where man is supreme; the law of increasing returns operates. But where the influence of the two is equally balanced, we shall have neither increasing returns nor diminishing returns. Instead, we shall have constant returns.

In every industry, we find the influence of both man and nature. Nature controls the raw materials, while man directs the manufacturing side. If there is an industry where the cost of raw materials and the manufacturing costs are half and half, we can say that both man and nature influence equally. Such an industry would be subject to the law of constant returns.

A possible example of such an industry is the woolen blanket-weaving industry. Here the raw material (wool) is supposed to cost about as much as the other manufacturing costs put together. If, there is an integration of the extractive and manufacturing industries e.g., sugar-making and cane-growing, steel-making and iron-ore mining, dairying and agriculture— the law of constant returns may operate.

Here the two aspects of the industry are combined, viz., the agricultural aspect which is subject to the law of diminishing returns and the manufacturing aspect which is subject to the law of increasing returns. It is possible for these two tendencies to counter-balance each other with the result that the law of constant returns may operate.

We thus find that in every industry two tendencies are constantly at work, viz., one of diminishing returns and the other of increasing returns. Whenever the scale of production is increased, the cost of raw materials and other factors may go up on account of increased demand. This tends to raise the cost of production per unit, or to bring about the operation of the law of diminishing returns. But, the larger the scale, the greater the economies in the use of machinery, division of labour, buying and selling, research and publicity, etc.

These economies tend to lower the cost per unit and set in operation the law of increasing returns. If these two tendencies are evenly balanced, i.e., if one tendency neutralizes the other, we shall have the operation of the law of constant returns.

In actual life, however, either the tendency of diminishing returns is stronger, as in agriculture and other extractive industries, or the increasing returns tendency is stronger, as in most manufacturing industries. Thus, the operation of the law of constant returns is rather rare, and, if at all it operates, it lasts only for a short period of time. Then the returns either increase or decrease.

Not Three but One Law:

Actually, as we have said, there are not three different laws of production but one law, viz., the Law of Variable Proportions, known also as Law of Proportionality. According to this law, variation in the proportion of the factors used produces different results as regards the output produced. It is assumed that there is no change in the techniques of production.

Normally, as production is expanded, the return first increases, remains constant for a while and then diminishes. It happens in every industry and the duration of each stage is different according to the nature of the industry. In agriculture, for instance, the stage of increasing returns is comparatively shorter, whereas, in industry, it is much longer.

In fact, a wise manufacturer may not let diminishing returns set in at all. Thus, there are not three laws but three stages of one law, viz., and the law of variable proportions. The variation in returns is not due to the change either in the prices of factors of production or in the price of the output. It is rather due to technological facts underlying production of the commodity in question.

Each industry has its own peculiar set of technical facts. For example, agriculture is dominated by land or nature, hence diminishing return sets in early. In manufacturing industries, man and machinery are supreme and the diminishing return may, therefore, be considerably delayed.

Three Aspects of the Law of Variable Proportions:

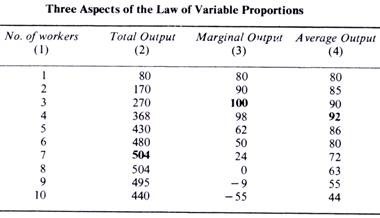
The operation of the law of variable proportions can be seen in three aspects, viz., variation in total output, average output and marginal output. Take the following table: The table given on p. 193 shows the behaviour of the total output, the marginal output and the average output as under

Total Output:

The total output is shown in column 2. We see that the total output begins to diminish from the 9th worker. Every successive worker employed makes addition to the total product up to the 7th worker.

But the 8th worker adds nothing and the 9th and 10th workers seem to be a positive nuisance. Instead of adding to the total output, they decrease it. Hence, in a situation represented by this table, no prudent employer will employ more than 7 workers.

Marginal Output:

We notice that the marginal output goes on increasing up to the 3rd worker, then it goes on falling till it reaches zero with the employment of the 8th worker. The 9th and 10th workers seem to cause only obstruction and make the marginal output negative. It can be seen that the total output reaches the maximum when the marginal product is zero.

Average Output:

The table shows that the average output reaches the maximum at the 4th worker, i.e., one step later than the marginal product reaches the maximum. It shows that it is possible for the average output to increase while the marginal output falls.

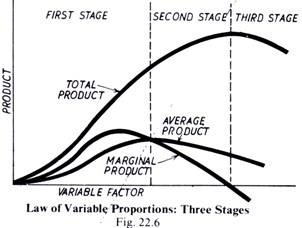
The three stages showing the behaviour of output, when varying quantities of a factor of production are combined with a fixed quantity of some other factor, are shown below in Fig. 22.6. In this figure, the quantities of the variable factor are measured along the horizontal axis OX and the total product, average product and marginal product are measured along the vertical axis OY.

It will be seen that the total product goes on increasing up to a point and teen it declines. The average product and the marginal product also increase and then decline. However, the marginal product starts declining earlier than the average product.

This type of behaviour of the total, average and marginal products can be divided into the following three stages:

Stage I:

In the first stage, the total product increases first at an increasing rate and then at a diminishing rate. The average product continues to rise throughout this stage, while marginal product first rises and then begins to fall until it equals the average product at the end of this stage.

Stage II:

In the second stage, the-total product continues, to increase at a diminishing rate till it reaches its maximum value. During this stage, both the marginal and the average-products-of the variable factor is decreasing but remain positive. The limit of the second stage is reached when the marginal product of the variable factor- becomes zero. This stage is the stage of diminishing returns and is the stage where a rational producer seeks to produce.

Stage III:

During the third stage, the total product declines and, therefore, the total product curve take a down-turn. The marginal product starts getting negative values, and, therefore, the marginal product curve goes below the horizontal axis. This stage is called the stage of negative returns.

It may be clearly understood that in this law, when production is sought to be increased, at least one factor of production is kept constant, while the quantities of the other factor or factors are increased. In this way, the proportion among the factors of production change’s then more output is sought to be produced. Hence the name of this-law—the “law of variable proportions”.

So long as the proportion among the factors of production goes on becoming more and more favourable, the marginal product or the marginal return will go on rising. But, as soon as the factor-proportion becomes unfavorable, the marginal return starts diminishing.

Since at least one factor (land or organization) may be constant, and only the other factors can be increased, the factor proportion is bound to become unfavourable sooner or later, and, when that happens, the marginal product or return must start diminishing. That is why some economists have given it the name of “the Law of Eventually Diminishing Returns”.