In sharp contrast to risk-averse individual, the risk lover or risk preferred will play a gamble.
A risk lover prefers uncertain outcome having the same expected value of income to the equivalent income with certainty.
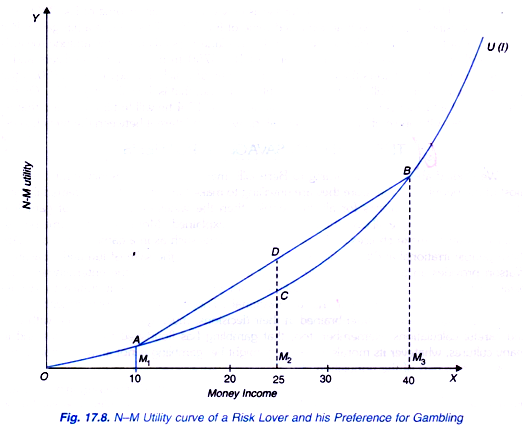
In case of risk preferring or loving individual, marginal utility of money increases as his income increases. In fig. 17.8 the N-M utility curve of a risk lover has been drawn that is convex.
The convexity of the utility curve implies that marginal utility of money income increases as his money income increases. Now suppose that present income of the individual is 25 thousand rupees and is offered a gamble with 50-50 chance of winning or losing Rs. 15 thousand rupees. Therefore, if he wins, his money income will rise to Rs. 40,000 and if he loses, his money income will fall to Rs. 10 thousand rupees. The expected money value of the gamble is given by.
ADVERTISEMENTS:
E(X) = 0.5 x 40,000 + 0.5 x 10,000
= 20,000 + 5000
= 25,000
In order to find out the expected utility of 25 thousand rupees we draw a chord AB which connects the utility M1A at income of Rs. 10 thousand and utility M3B at income level of Rs. 40 thousand. Corresponding to the expected value of income of Rs. 25 thousand the expected utility is M2D whereas point D lies on the chord AB corresponding to income of Rs. 25 thousand. It will be seen from Fig. 17.8 that expected utility M2D of expected income of Rs. 25 thousand is greater than the utility M2Cof certain income of Rs. 25 thousand.
Since his expected utility from gamble is greater than that from his income with certainty, he will accept the gamble. Further, it can be shown that risk lover, a person whose marginal utility of money increases with increase in his income will prefer a gamble having greater risk, that is, the gamble which has a larger variability of outcome to a gamble with less risk (that is,’ with smaller variability of outcome).
An Application: Fanner’s Gambling Against Nature:
We will now provide an interesting and useful application of choice under risk and uncertainty to the case of a farmer who in the absence of irrigation has to face an uncertain situation regarding outcome of his use of fertilizers which yields higher output only in the presence of water, the availability of which, in the absence of irrigation, depends on the rain.
If the farmer fertilizes his land and nature is kind and there is good and timely rainfall, he will reap a bumper crop. On the contrary, if it does not rain, his output (and therefore his income) will be low because the use of fertilizers in the absence of water is likely to burn his seed and damage his soil. If the farmer does not use fertilizers, he will have a moderate but a certain income. Thus the farmer for deciding whether or not to fertilize the land is playing a game against nature.
ADVERTISEMENTS:
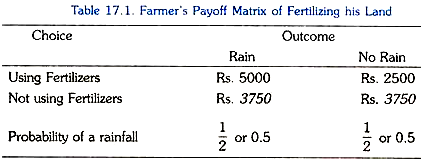
Let us illustrate it with a numerical example. Suppose if our farmer uses fertilizer his income rises to Rs. 5000 but only if there is a good rainfall. And if it does not ram, his output or income will be small because in the absence of water, the use of fertilizers may destroy much of his seed and also cause damage to his soil. Let his output or income in this case comes about to be Rs. 2500.
Suppose in the case of non-use of fertilizers, he has a modern e output worth Rs 3750 regardless of whether it rains or not. What choice a farmer will make under this uncertain situation depends on his attitude towards risk. To know this we have constructed a pay off matrix of the farmer which is given in Table 17.1. It is further assumed that the farmer expects that there is 50:50 chance of rainfall.
The choice of not using fertilizers yields a certain income of Rs. 3750. The choice by the farmer in favour of using fertilizers yields expected value equal to 1/2 (5000) + 1/2 (2500) = Rs. 3750. Thus the choice facing the farmer is between a certain income of Rs. 3750 and a gamble of using fertilizers with an expected value of Rs. 3750.
This is quite a fair game. But whether or not the farmer will choose to fertilize his land depends upon his attitude towards risk. His choice is between a certain income of Rs. 3750 from not using fertilizers and a gamble of using the fertilizers the expected money value of which also equals Rs. 3750.
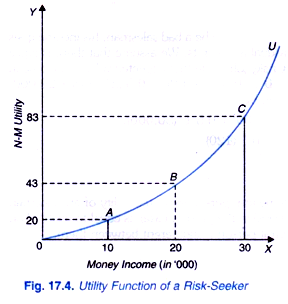
If the farmer is risk averter, he will choose not to fertilize the land, that is, he will not gamble. On the other hand, if a farmer is risk lover, as depicted in Figure 17.4 he will fertilize the land that is, he will gamble. Of course, if he is a risk neutral, he will be indifferent between the two choices.’