The laws of returns are often confused with ‘returns to scale’.
The two maybe clearly distinguished. By “returns to scale” is meant the behaviour of production 6r returns when all the productive factors are increased or decreased- simultaneously and in the same ratio.
In other words, in returns to scale, we analyse the effect of doubling, trebling, quadrupling, and so on of all the inputs of productive resources on the output of the product.
The returns to scale may clearly be distinguished from the Law of Variable Proportions, in which while some co-operating factors of production may be increased, (or decreased), at least one factor (e.g., land in agriculture) remains constant or cannot be increased (e.g., the entrepreneur in industry), so that the proportion among the factors of production changes and we see how returns or output is affected by such changes in the supply of the productive resources.
ADVERTISEMENTS:
In returns to scale, on the other hand, all the necessary factors of production are increased/decrease to the same extend so that whatever be the scale of production, the proportion among the factors remains the same.
Three Phases of Returns to Scale:
A layman, uninitiated into the techniques of economic analysis, would perhaps expect that, with the doubling of all productive factors, the output would also double and with trebling of all factors of production, production would also be trebled, and so on. But actually this is not so. In other words, actually the output or returns do not increase/decrease strictly according to the change in the scale. We know that in the case of the Law of Variable Proportions, as we increase some of the co-operating factors, the marginal product or returns increases at first, and then stays constant and ultimately it starts diminishing.
Similarly, when we increase the scale, i.e., all the factors of production together to the same extent, the marginal product or return increases at first, i.e., up to a point, then stays constant for some further increases in the scale, and ultimately starts declining when the scale of production is increased still further. In other words, there are three distinct phases of, or stages in, the behavior of the marginal product.
ADVERTISEMENTS:
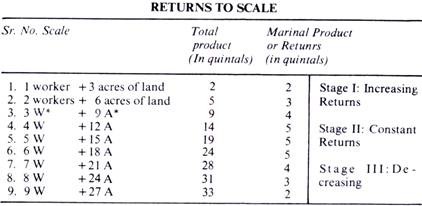
Let us take a numerical example to explain the behavior of the returns to scale in the table below:
‘W’ stands for Workers and ‘A’ stands for Acres of land.
In the above table, we see that at the outset when we employ one worker on three acres, of land, the total product is 2 quintals. Now to increase output, we double the scale, but the total product increases to more than double (to 5 quintals instead of 4 quintals) and when the scale is trebled, the total product increases from 5 quintals to 9 quintals—the increase this time being 4 quintals as against 3 in the previous case.
ADVERTISEMENTS:
In other words, the returns to scale have been increasing. If the scale of production is further increased, the marginal product remains constant up to a certain point and, beyond it, it (the marginal product) starts diminishing. In the above table at Serial No. 9 the marginal product or return falls to only two quintals.
Explanation:
Now we may try to explain why we get the above-mentioned three phases or stages, i.e., what makes the returns to scale behave in the manner they do. The chief reason of this kind of behaviour is that when, in the beginning, the scale of production is increased, increased division of labour becomes possible and is adopted and, as a result thereof, output increases rather rapidly.
In the above table, when there is only one worker working on three acres of land, there is no scope for division of labour. When there are two workers instead and six acres of land, i.e., the factors of production are doubled, there will be scope for division of labour and the output will not only double but increase still more, and the returns to scale too will increase.
In this way, up to a certain point, the returns to scale will go on increasing until there is no further scope for division of labour. Beyond this point, the marginal product or the returns to scale will cease to increase and will remain constant for certain further increases in scale (e.g., in the above table when 5 workers and 15 acres of land are used instead of 4 workers and 12 areas of land; the marginal product remains 5 quintals as before; similarly for Serial No. 5 to Serial No.6).
But when scale is increased beyond Serial No.6, the scope for division of labour is reduced with the result that the marginal return or product begins to decline. In short, the main underlying cause of the changing returns to scale is the possibility or otherwise of the division of labour or specialisation.
However, it is very important to state here that, in actual life, the scale of production cannot be increased beyond a certain limit. To increase the scale of production means that all factors being used in production can be increased at will and indefinitely. But it is not so in practice. While land, labour and capital can be increased, the entrepreneur or organiser remains the same.
In other words, there is at least one factor of production which cannot be varied at will and hence, when more output is desired, the proportion among the factors of production used must change. Hence, the returns to scale are more of theoretical interest than being relevant to actual life. In practice, it is the law of variable proportions, on the other hand, which is universal application.