Most people are risk averters and therefore they buy insurance to avoid risk.
Now an important question is how much money or premium a risk-averse individual will pay to the insurance company to avoid risk and uncertainty facing him.
Suppose the individual buys a house which yields him income of Rs. 30 thousands per month. But if the house catches fire and due to the damage caused, his income from it falls to Rs. 10 thousands per month and thus he suffers a loss of income. For the sake of simplifying analysis suppose there is 50 per cent chance of the house catching fire. Then they expect value of income in this risky and uncertain situation is
E (X) = 0.5 X 30,000 + 0.5 x 10,000
ADVERTISEMENTS:
= 15,000 + 5,000
= 20,000
It is important to note that expected income of Rs. 20,000 is the weighted average of the two uncertain alternatives (30 thousands and 10 thousands) using their probabilities as weighty Different probabilities of the occurring of these incomes (30 and 10 thousands) would yield different expected income. Further note that the expected income is not the actual income that a person would get; it is weighted average of the two uncertain outcomes.
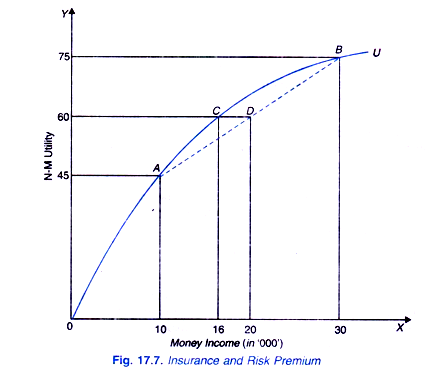
The utility function OU with a diminishing marginal utility of money income of a risk- averse individual is shown in Fig. 17.7. With money income of Rs. 30 thousands, his utility is 75 and with his lower income of 10 thousands his utility is 45. Given that there is probability of 0 5 for each outcome, expected utility of the two outcomes is given by
ADVERTISEMENTS:
E (U) = 0.5 U (30,000) + 0.5 U (10,000)
= 0.5×75 + 0.5 x 45
= 37.5 + 22.5
= 60
ADVERTISEMENTS:
It will be seen from Fig. 17.7 that we have drawn a straight line AB joining the utilities of 75 and 45. It is on this straight line or chord AB that the amount of expected utility will be corresponding to the expected value of income in the present risky and uncertain situation it will be seen from Fig.17.7 that on this straight line AB and corresponding to the expected value of income of Rs. 20 thousands, the expected utility is 60 which corresponds to Point D on the straight line AB.
But it will be seen from the individual s utility function OU, that utility of 60 is equal to that of an assured and certain income of Rs. 16 thousands. Thus the individual with an expected uncertain income of Rs. 20 thousands will be willing to forego Rs. 4 thousands (or DC) to get a certain or guaranteed income of Rs. 16 thousands as the expected Utility of uncertain expected income of Rs. 20 thousands is equal to the utility of a certain income of Rs. 16 thousands.
This means that if the individual gives up Rs. 4 thousands (20 – 16 = 4) from his uncertain expected income he will get the same utility of 60 as with a certain income of Rs. 16 thousands. Rs. 4 thousands equal to distance DC is called the risk premium.
Therefore, the risk premium is the amount of money that a risk-averse individual will be willing to pay to avoid the risk. By paying the risk premium the individual can insure himself against a large loss from a fire and to get an assured or certain income. It is clear from above why people buy insurance for fire, accident, ill health and even life.