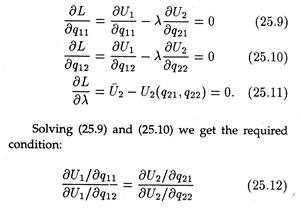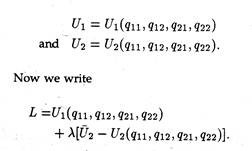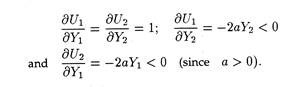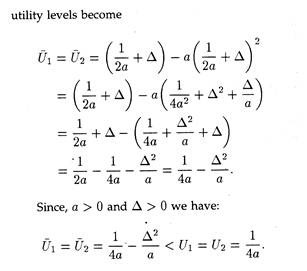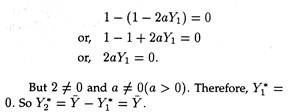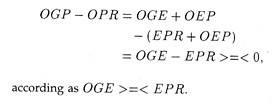Economic Externalities: Concept, Type and Control

In this article we will discuss about the Economic Externalities:- 1. Concept of Externality 2. A Formal Representation of Externality 3. Types 4. Consumption Externalities 5. Public Goods and Consumption Externali­ties 6. Control.

Contents:

1. Concept of Externality
2. A Formal Representation of Externality
3. Types of Externality Relationships
4. Consumption Externalities
5. Public Goods and Consumption Externali­ties
6. Control of Externalities

---

1. Concept of Externality:

In the context of theories relating to producer and consumer behaviour, the notion of “Pareto Optimality” has become very much popular. A situation is said to be Pareto Optimal if any redistribution of re­sources cannot make any individual better off, without hurting at least one person.

Therefore, satisfying the Pareto Optimality condition implies that the society has attained welfare maximization objective (i.e., both consumers and producers have maximized re­spective utilities and profits).

This notion of wel­fare maximization is based on the assumptions that there do not exist interdependences among produc­ers, among consumers and between producers and consumers.

Furthermore, it is also assumed that per­fect competition prevails in all the relevant markets. The logical corollary of all these assumptions is that all costs and benefits of economic agents (i.e., con­sumers and producers) are truly reflected in the mar­ket prices (that are incurred or received).

In this case, private benefits and costs equal social benefits and costs. However, in reality, the picture is not that rosy. Indeed, what we generally find is interdependences among different economic agents and hence, diver­gences between private and social benefits and/or costs.

This is the situation of ‘externalities’. So exter­nalities are said to exist when action(s) of economic unit(s) creates benefits and/or costs to third party (or parties), where the latter(s) is (are) a not direct par­ticipant.

More precisely, external effects exist when:

(a) Production or consumption of one party affects the production or consumption of other parties and

(b) The effect is un-priced or uncompensated (in the case of benefits, the benefits are non-appropriated or untaxed).

The first condition is the “interdepen­dence condition” and the second one relates to “price condition”. Externalities exist only when both the conditions prevail.

However, even if the latter condition is appropriately taken care of (i.e., price effect is eliminated), still we many say that externalities exist, only then, externality is said to be “internalized”. In this context, it should also be stressed that for externalities to occur, condition (a) is indispensable, i.e., in a sense, it is the necessary condition.

---

2. A Formal Representation of Externality:

In the absence of external effects, the utility of an individual depends not only on the amounts of goods he/she consumes, but also on the amounts of goods the other person consumes. Suppose there are only two individuals A and B, and two consumer goods, 1 and 2. Let X_ij be the amount of the j-th good that person i consumes, (i = A, B, j = 1, 2) and U_i be the utility function of person i.

Then, in the presence of externalities, we get:

U_A = U_A (x_A1, x_A2, x_B1, x_B2) and U_B = U_B (x_B1, x_B2, x_A1, x_A2)

Had there been no external effects, we would have:

U_A = U_A (x_A1, x_A2) and U_B = U_B (x_B1, x_B2).

Similarly, in the sphere of production, when ex­ternal effects exist, levels of cost and output (and hence profit) of any producer depends not only on his/her activity, but also on the activity levels of other producers.

---

3. Types of Externality Relationships:

If the economy is composed of only produc­ers and consumers, then there may be four types of externality relationship, viz.:

(a) Producer-Producer,

(b) Producer-Consumer,

(c) Consumer-Producer and

(d) Consumer-Consumer.

The first case refers to the situ­ation when action of one producer affects the other producers.

Suppose there are two wheat producers in adjacent farms, one of whom is relatively a larger producer. Assume, also, that there is a nearby well from which both the producers water their fields. Now, if the large producer increases his cropping intensity (say, due to improved technology which he can afford), he taps more and more water.

As a result the water table goes down in the well. The small producer may not now get an easy supply of water. His crops receive less water than previously. As a result the small producer may cut his produc­tion level, or if he maintains the same production level, shortage of water may cause the quality of wheat to fall. The reverse could also happen.

The large producer could, at his own cost and in his own interest, dig a well within his farm to become totally self-sufficient. In that case, the small producer him­self would use the old well alone, which is definitely beneficial to the latter individual.

In reality, on the other hand, producer-consu­mer externality relationship is very common. The smoke that is emitted by the chimneys of a steel producer pollutes the air and affects the inhabitants’ (who are also consumers) health.

The third case, i.e., consumer-producer relationship is, however, not so evident whereby consumers’ actions affect produc­ers’ behaviour. Such a relationship perhaps may ex­ist on the demand side where the consumers’ tastes, incomes, etc. have an impact on the producer.

We all know that the Philips Company produces a variety of electrical and electronic goods, notably radio, T.V., tape-recorders, bulbs, etc. If our consumers begin to switch their demands from radios to T.V.s and/or tape-recorders, the company would then find it appropriate to curtail radio-manufacturing and instead concentrate on producing T.Vs and/or tape-recorders.

The fourth and final type, i.e., consumer-consumer relationship, exhibits the case where the action of one consumer affects others. Here we may distin­guish between ‘envy’ and ‘non-envy’ externalities.

In the former case the consumer is envious of oth­ers’ welfare increase to be more precise, increase in others’ utility leads to a loss of the concerned consumer’s utility. We may view this as a sort of ‘demonstration effect’. The non-envious externali­ties, on the other hand, are quite common.

Sup­pose an individual A purchases a stereo and plays it in a high volume. The person derives some util­ity from this, but the noise may cause disturbance to the next-door neighbour, individual B. Suppose B’s recreation is reading. He cannot concentrate on his reading as a result of this disturbance. Surely B’s utility is reduced as a result of the noise created by A’s stereo.

---

4. Consumption Externalities:

In the absence of consumption externalities, the utility functions of the consumers are not inter­dependent; rather, they are independent. In such sit­uations, Pareto optimality requires that the marginal rate of commodity substitutions (MRCS) be equal among the individuals.

With the advent of external­ities, this condition changes and accordingly a mod­ified result is obtained. Let there be two consumers only, 1 and 2, and their respective utility functions be U₁ and U₂. Also assume that there are two goods, q₁ and q₂ and q_ij is the consumption of the j-th good by the j-th consumer.

When externalities are absent, the utility functions are:

U₁ = U₁ (q₁₁, q₁₂) and U₂ = U₂ (q₂₁, q₂₂)

q₁₁+ q₁₂ = q₁ and q₁₂ + q₂₂ = q₂.

To obtain the condition for Pareto optimality we maximize the following Lagrangian expression:

where λ is the associated Lagrange multiplier.

The F.O.Cs for maximization are:

Where ∂U_i/∂q_ij is the marginal utility (MU) for good j of individual i. (25.12) has been attained in the non- externality case. Now let us see how (25.12) changes when we allow for externalities.

Utility functions now become:

The ‘Envy Effect’:

We have earlier defined envious consumption externalities whereby an increase in i-th consumer’s utility causes a reduction in the j-th consumer’s util­ity. Let us consider this ‘envy effect’ with the help of a formal model. Suppose there are two consumers, 1 and 2, and on good Y where Y_i is the level of the consumption by ith person.

In the presence of envy the utility functions are:

Here a > 0.

Here (∂U_i/∂Y_i) is the MU of consumer i due to the increase of his/her consumption and ∂U_i /∂Y_j (I ≠ j) is the change in MU of consumer i as a result of increase in other’s consumption. Note that

Also note that as long as a ≠ 0, consumption externalities exist. To find out the socially optimum level of consumption, we maximize

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

It is evident that after the distribution of surplus each person’s utility diminishes; so social welfare also falls. Hence, in the presence of consumption externalities in the form of “envy effects” it would be wise for the government not to distribute the surplus at all and let the surplus persist. Suppose now that individual 1 is free from envy; however, individual 2 is envious. The utility functions are, therefore,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

From (25.20) we obtain λ = 1 – 2aY₁. Putting the value of λ in (25.21) we get

 

 

 

 

Therefore, society does not allow individual 1, who is absolutely free from envy, to consume any­thing. What a tragedy for a non-envious person, in­deed! (be envious then, or you will receive nothing). When Y₁ changes, the net effect on social welfare is

On the other hand, when Y₂ changes the net effect on social welfare is ∂U₂/∂Y₂ = 1

Clearly 1 > 1 — 2aY₁, i.e., society gains more when Y₂ changes, compared to Y₁. Suppose due to change in Y₁, the first person’s utility increases by 1 unit and the second person’s utility falls by ½ unit. So there is a net increase in social utility of ½ unit. The first person, unlike the second, is free from envy.

Therefore, if the second individual’s utility increases by 1 unit, there is no impact on individual 1. Hence, social welfare increases by 1 unit, which is greater than ½ unit. Thus, it is always beneficial to raise envious person’s consumption (and hence utility). And that is why social optimality is reached when Y₁* = 0 and Y₂* = Y (continuously increasing Y₂ and diminishing Y₁).

The cause of this apparent paradoxical and un­fortunate result is that the society treats both indi­viduals’ utility equally, i.e., equal weight have been placed against U₁ and U₂. Had the society consid­ered that consumer 1 is not envious and accordingly placed different weights, the result would not then be surprising.

---

5. Public Goods and Consumption Externali­ties:

A different type of externality exists when pub­lic goods enter the consumption bundle of the con­sumer. The distinctive feature of public goods is that consumers can consume them collectively and in equal amounts so that one’s consumption does not lead to reduced availability to the other.

Also, since everybody can consume public goods equally, it is beneficial for everybody to conceal his/her true preferences. For this reason, the prices of public goods cannot be evaluated like private goods.

In the non-externality case, the overall Pareto optimality condition is that MRCS and MRTS (marginal rate of technical substitution) for all con­sumers and producers must be equal for every pair of goods. When we incorporate public goods in the system (which bring in externalities), the above stated condition does not hold. Let us investigate the matter in terms of a simple model.

The Model:

There are two consumers, 1 and 2, two private goods, x₁ and x₂, (distributed between the two consumers) and one public good Y (which is consumed in equal amounts by both). We denote X_ij as the amount of the j-th good that the individual i consumes. On the basis of this information we may write

X₁₁ + x₂₁ = x₁, x₁₂ + x₂₂ = x₂

and Y₁ = Y = Y₂,

where Y_i is the consumption of the public good by the i-th consumer.

We assume that consumers have well-behaved preference orderings with respect to their consump­tion levels of x₁, x₂ and Y (i.e., well-behaved utility functions).

Then, we have

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

We see, therefore, that when public goods are present in production and consumption, welfare maximization yields not one, but two sets of con­ditions, viz., (I) and (II) In non-externality case, (I) is present, but (II) cannot be obtained. Thus, there is no single optimality condition, but a set of such conditions.

---

6. Control of Externalities:

Externalities are of two types—external economies and external disecono­mies. While the former is beneficial to economic agents’ interests, the latter is detrimental to their (and society’s) interests.

Therefore, external econo­mies do not require control. However, for the wel­fare of society, diseconomies should be controlled. The control may be exercised either by the government or the parties creating and receiving these ef­fects may come forward voluntarily to check the ad­verse side effects. There are various ways in which this can be accomplished.

These are briefly discussed below:

1. Prohibition:

Suppose a jute industry exists in the vicinity of the city. The industry is polluting the air, which obviously has a social cost. The government may prohibit the industry’s production and check air pol­lution (for which the industry pays nothing). How­ever, total prohibition is not perhaps feasible. Pro­hibition should be enforced in some other way.

2. Directive:

The government may circulate directives stressing the need to keep the environment clean. The problem is that directives are not binding; hence they are often ignored.

3. Taxes and Subsidies:

Much have been said on it earlier. Only it should be remembered that taxes and subsidies are not only imposed on producers, but also on con­sumers. Consider the case of liquor consumption. By consuming alcohol, drunk drivers can cause ac­cidents, which may result in damages, deaths, etc.

These are definitely external diseconomies of con­sumption. To stop these casualties, if the govern­ment taxes both producers and consumers, then pro­duction and consumption of alcohol would fall.

4. Sale of Pollution Rights:

When producers pollute the environment, the government may auction off pollution rights. Auc­tion of pollution licence by the government will lead to competition among the producers (i.e., the buy­ers) so price of licence will increase as also the costs to the firms. To avoid this cost, the firms may try to check pollution in advance in their own interests.

5. Regulation:

The government can regulate external disecono­mies by passing laws. Scooter accidents often cause a lot damages to scooterists (and public). To reduce these damages, the government may make (and does make) wearing helmets a must for the scooterists.

6. Merger:

This can be explained by an example. Suppose a chemical plant exists beside a river. It discharges wastes from the factory into the river; so the river water gets polluted.

In the downstream, a paper mill is situated which uses this river water. The pol­luted water makes the quality of paper inferior. This is a loss to the paper mill. This loss is caused by the chemical factory, but it does not pay the paper mill to compensate for the loss.

Under such circumstances the two firms may merge and become one firm pro­ducing two different products. The profit of the firm depends on both these products. Therefore, to make superior quality paper, the chemical unit will try to keep the water pure.

7. Voluntary Payment:

By this method external diseconomies can be avoided if the parties creating them voluntarily pay to those who are suffering from diseconomies. In reality it is, however, hard to accept.

8. Negotiation:

Consider the example where the chemical plant generates external diseconomies for the paper mill.

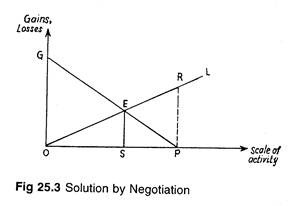
In fig 25.3 we measure scale of chemical plant’s activity on the horizontal axis (let this be Firm A) and its gains and losses on the vertical axis. Due to the activity of Firm A, the paper mill (Firm B) incurs a cost.

GP is A’s marginal net gain (MNG) function, and OL is the corresponding marginal net loss function (MNL) function of B. If A is a profit maximize, his profit maximizing activity level is OP where his MNG = 0. At this level of activity, A’s total gain is OGP and B’s total loss is ORP. There­fore, the net social gain is

 

 

 

 

Now, suppose A and B negotiate and reach an agreement. Then A will cut back his activity level from P to S. At this level, the net gain of society is

OGES – OES = OGE.

Clearly, negotiation has raised social gains. However, one thing must be noted. Negotiation has no doubt raised welfare, but it has not elimi­nated the diseconomies altogether; it has only elim­inated a part of ‘Pareto relevant’ diseconomies, viz., ESPR.

To avoid adverse side effects totally, the best thing is perhaps to switch over to a new superior technology which can eliminate them. One should also note that such negotiations can be fruitful only if A and B possess equal bargaining power, or B can convince A to choose the activity level at point S.

---