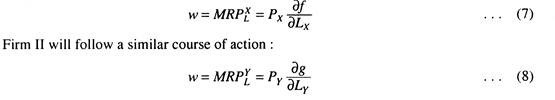Economic Externalities: Meaning, Types and Effects!
Meaning and Definition:
Externalities occur because economic agents have effects on third parties that are not parts of market transactions. Examples are: factories emitting smoke and did, jet plains waking up people, or loudspeakers generating noise. These activities are all having a direct effect on the well-being of others that is outside direct market channels.
In these cases market prices (of soaps, air travel and entertainment) may not accurately reflect social cost because they take no account of the damage being done to third parties. Information being conveyed by the prices is fundamentally inaccurate, leading to a misallocation of resources.
An externality occurs whenever the activities of one economic agent affect the activities of another agent in ways that do not get reflected in market transactions. This is why externalities are taken as examples of market failure.
Types of Externality:
Externalities are of different types. Here we consider four main types of externality
(I) Inter Firm (Production) Externalities:
ADVERTISEMENTS:
Suppose there are two firms in the economy — firm I is producing X and firm II is producing Y. Each uses only single input, labour. The production of good Y is said to have an external effect on the production of X if the output of X depends not only on the amount of labour chosen by firm I but also on the level at which the production of Y is carried on. In this case the production function for good X can be expressed as
X = f (Lx ,Y) .. (1)
where Lx denotes the amount of labour used to produce and Y indicates an effect on production over which firm I has no control. Negative inter-firm (or firm-firm) externality exists if ∂X / ∂Y < 0, i.e., increase in output of Y causes less of X to be produced.
(II) Beneficial Externalities:
ADVERTISEMENTS:
The activity of one firm may also have beneficial effect on others. For example, if a power plant is set up near a coal mine, hopefully, more coal can be extracted due to an abundant supply of power. In this case, ∂X/ ∂Y > 0. However, in the usual perfectly competitive case, the productive activities of one firm have no direct effect on those of other firms: ∂X/∂Y= 0.
(III) Externalities in Utility (Consumption Externalities):
Externalities also can occur if the activities of an economic agent directly affect an individual’s utility. Most obvious examples are environmental externalities (such as noise from a loud radio). Such externalities may sometimes be beneficial.
(Mr. John may actually enjoy the song being played on Mr. Sen’s radio) this type of externality arises when one individual’s utility depends directly on the utility of someone else. If, for example, Mr. A cares about Mr. B’s welfare, we can express A’s utility
UA= f (XuX2,…,Xn; UB)……(2)
where X1X2 ,… Xn are the goods which A consumes and UB is B’s utility.
ADVERTISEMENTS:
If A wants B to be better-off (if A were a close relative of B, ∂UA/∂UB would positive. If, on the other hand, A were envious of B, ∂UA /∂UB would be negative; that is improvements in B’s utility make A worse off. If A were indifferent to B’s welfare, ∂UA/∂UB = 0.
(IV) Public Goods Externalities:
Public goods or collective consumption goods (such as national defence, roads, bridges, public parks, public school, hospitals, etc.) create externality problems because such goods can be allocated through the market and those who enjoy such goods do not pay prices directly.
The cost of providing such goods is covered through taxes. Once such goods are produced (either by the government or by some private agency) they provide benefits to all the members of society. This is because such goods are to be consumed jointly. It is not possible to restrict these benefits to the specific group of individuals who pay for them.
So the benefits are available to all. For example, once a national defence system is established, all individuals in society are protected by it—whether they wish to be or not and whether they pay for it or not. Choosing the right level of output for such a good is a complex task, since market signals are not quite accurate.
Effects of Externalities:
Externalities create divergence between social benefit and private benefit and between social cost and private cost. In the presence of positive externality, marginal social benefit (of any activity such as education or health/medical care) = marginal private benefit + marginal external benefit.
This is why, in the presence of positive externality, a commodity or service is under produced – its actual output is less than the socially desirable level. And there is need to subsidies all activities which generate positive externalities and cause departure from Pareto optimality.
Likewise, in the presence of negative externalities, marginal social cost = marginal private cost + marginal external cost. As result a commodity or service is overproduced. Actual output exceeds the socially desirable level, the activity generating negative externality has to be taxed in order to ensure Pareto optimality.
Externalities and Allocative Efficiency:
The presence of externalities can cause a market to operate inefficiently. This point may now be illustrated. Let us assume that two firms are located near each other and that one of these (II) has negative effect on the production of the other (I). Suppose the production function of the firm II which generates pollution is expressed as
Y = g(LY) … (3)
ADVERTISEMENTS:
where LY = the quantity of labour devoted to the production of Y. The production function for good X (which exhibits an externality) was given by equation (1). The Pareto conditions for an optimal allocation of labour require that the social marginal revenue product of labour (SMRPL) be equal for both firms. If Px and PY are the prices of good X and good Y, respectively, the SMRPL in the production of good X is given by
Due to the presence of production externality, the statement of the SMRPL in the production of Y is more complex. An extra unit of labour employed by firm II will produce some extra Y.
But it will also generate some extra pollution, and will reduce the output of AT, produced by Firm I, Consequently,
ADVERTISEMENTS:
where the second term on the right hand side represents the effect of hiring additional workers in the production of K on the value of production of X. This effect will be negative if ∂f/∂Y< 0 Efficiency then requires that
Independent decision-making by the two firms will normally not ensure the fulfillment of this condition. Firm 1 (producing X) will hire labour up to the point at which its private MRP, is equal to the prevailing wage rate
ADVERTISEMENTS:
The market will, therefore, equate private marginal revenue products, but this market equilibrium will ensure Pareto efficiency only if ∂f/∂Y = 0 in equation (5). In other words in the presence of externalities, the decisions of the two firms or their managers will not bring about an optimal allocation.
Since we have assumed that ∂f/ ∂Y< 0, labour will be over allocated to the production of good Y. The SMRPL in the production of Y will fall short of that in the production of X. If, on the other hand, we assume that ∂f/∂Y> 0, then labour will be under-allocated to the production of Y.
Solving the Externality Problem:
There are certain solutions to the allocation problems posed by externality.
Two such solutions are taxation and merger:
1. Taxation:
The government can impose a suitable excise duty on the firm generating the external diseconomy. This tax is likely to cause the output of Y to be cut back and would cause labour to be shifted out of the production of Y. This standard remedy was first suggested A. C. Pigou in the 1920s and is known as the Pigouvian tax.
ADVERTISEMENTS:
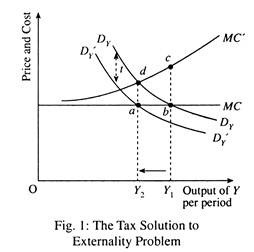
The taxation solution is illustrated in Fig. 1. The demand for Y is given by DY D Y and the private marginal cost curve for Y by MC. The curve MC’ shows the social marginal cost of production of Y. Thus the socially optimal level of output is Y2. However, in the presence of negative externalities, the normal functioning of the market will cause output level of Y1 to be produced.
One way to force the market to allocate goods correctly would be to impose an excise duty of t per unit of Y produced. The effect of this indirect tax is to shift the demand curve facing the firm from DYDY to D’YD’Y and this will cause the profit maximising the level of output of Y to fall from Y1, to Y2. This is a government solution to the externality problem.
2. Merger and Internalization:
A private solution for the allocational distortions caused by the externality between X and Y would be for the two firms to merge. If a single firm operates both plants X and Y, it will recognise the harmful effect that production of Y has on the production function for good X.
In effect, the new (merged) firm would now bear the full social marginal costs of Y production because it also produces X now. In other words, the firm would now take the marginal cost curve for Y production to be MC’ in Fig. 1 and would produce at the point where
Py = MC’ … (9)
ADVERTISEMENTS:
which is exactly what is required for allocative efficiency.
The externality in the production of Y has been internalised as a result of the merger. The reason is that what was marginal external cost before the merger has now become a part of the marginal private cost of the merged firm.