Total Revenue (TR) and Elasticity (With Diagram)

Total Revenue (TR) and Elasticity (With Diagram)!

It may be recalled that the demand for a commodity is said to be price elastic if total reve­nue increases (falls) as price increases (falls). And if TR remains constant whether P falls or rises, de­mand is said to be unitary elastic.

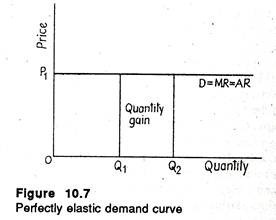
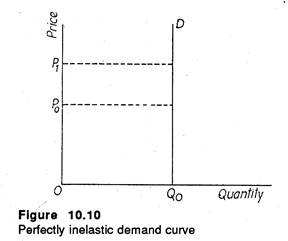
We have noted that the slope of the demand curve is not the same as its elasticity. However, only in two situations we can calculate elasticity from slope alone, viz., completely elastic demand (a horizontal straight line in which case dP/dQ = 0) and completely inelastic demand.

In Figure 10.7 we have shown a perfectly elastic demand curve. In figure 10.10 we show an exactly opposite type of de­mand curve, viz., a perfectly inelastic (a vertical straight line) demand curve. In this case an un­changed quantity can be sold at all possible prices (such as OP₀, OP₁, etc.). This usually happens in case of highly necessary goods like cigarettes, salt or life-saving drugs.

When the prices of such products fall, there is not much fall in quantity demanded. This is why the Finance Minister often imposes high rates of sales tax or excise duty on such goods. The tax is initially imposed on the producer but is subsequently passed on to the consumer in the form of higher price.

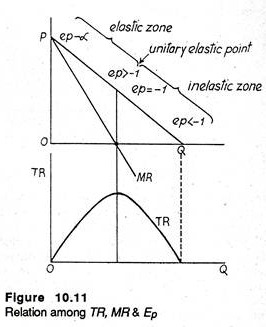
In fact, values of price elasticity can be in the range 0 to – ∝ Values from 0 to -1.0 lie in the ine­lastic zone of the demand curve. In this zone per­centage increases in Q (which raise revenue) are not as great as the corresponding percentage decreases in P (which lower revenue). Therefore, TR falls as price is reduced. Look at the following demand and corresponding TR curves.

Three points are illustrated by Figure 10.11.

(a) When E_p > -1, i.e., demand is inelastic, TR in­creases as P rises and MR is positive.

(b) When E_p = -1, i.e., demand is unitary elastic, TR is constant as P falls, and MR is zero.

(c) When E_p < -1, i.e., demand is inelastic, TR falls as P falls, and MR < 0.

So if the demand for a firm’s product is inelastic (i.e., 0 < E_p > -1) one should not reduce price to raise revenue. Rather the only way of raising revenue is to raise price. But if demand is elastic (i.e., -1.0 < e_p < ∝) per­centage expansion of quantity exceeds percentage contraction of price. So TR rises as P falls.

However, it may be noted that even if demand is elastic a firm may not gain by reducing price and increasing quantity. In-fact, increase in output and sales implies an increase in both revenue and cost of production.

The business manager’s price and output decisions do depend on comparison of MR with mar­ginal cost (i.e., the extra cost of producing an addi­tional unit). If demand is unitary elastic, there is no scope for raising TR either by reducing P or by raising it. So the only way of raising TR is to reduce cost of production per unit of output (by raising or reducing the volume of output).