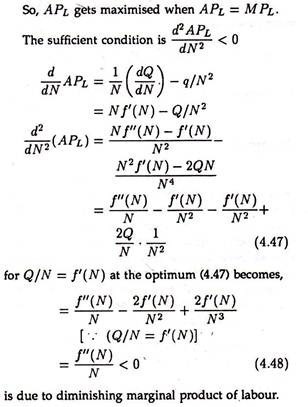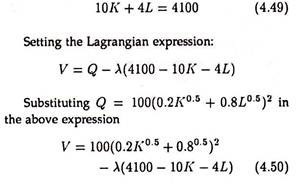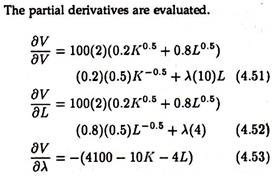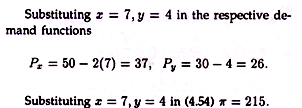Here we are going to deal with some optimisation problems.
(a) In section 4.2 while dealing with average product and marginal product, we have shown graphically that when APL attains maximum, APL = MPL.
This can be shown by calculus. We define the production function as:
The sufficient condition for maximisation holds. Therefore, when APL is maximum, APL = MPL.
(b) Given the production function Q = 100(0.2 K0 5 + 0.8L0.5)2, and prices of per unit capital and labour are 10 rupees and 4 rupees respectively. If the manager is further given a sum of Rs. 4,100 as expenditure for production, then find the optimal values of capital and labour which will maximise production.
The problem is to maximise Q subject to a given level of cost (Rs. 4,100).
The cost equation:
The partial derivatives are set equal to zero, which is the first order condition.
(c) A monopolist sells to products x and y, for which the demand is
ADVERTISEMENTS:
x = 25 — 0.5Px, y = 30 = 30 – Py,
and the combined cost function is
c = x2 + 2xy + y2 + 20.
Find (a) the profit maximising level of output for each product (b) the profit maximising price for each product and (c) the maximum profit