The Loanable Funds Theory of Interest | Microeconomics

The neoclassical theory of interest rate determination is named the loanable funds theory. The exponents of this theory are the neoclassical economists like Wicksell (1851-1926), Ohlin (1899-1979), Robertson( 1890-1963), Myrdal( 1898-1987), Lindahl and Viner (1892-1970). The loanable funds theory contends that the rate of interest is determined by the demand for and supply of loanable funds.

Supply of Loanable Funds:

The sources of the supply of loanable funds are:

(i) Saving from Disposable Income:

Savings of the individuals and households from their present disposable income (i.e., after-tax income), is the chief source of loanable funds. It is assumed here that, as the income of the country rises, the savings of the households also move upwards.

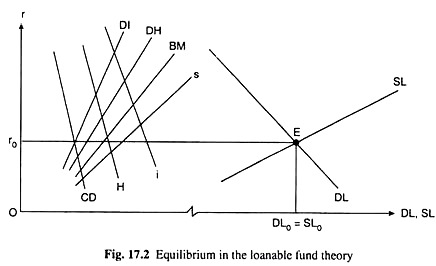
Again, saving also rises as the rate of interest rises. In other words, it is assumed here that saving is an increasing function of income and rate of interest. Therefore, income remain­ing constant, as the rate of interest rises or falls, saving also increases or decreases, respec­tively. Therefore, the saving function or the saving curve, s, would be upward sloping like one shown in Fig. 17.2. This curve tells us s at any particular r.

(ii) Dishoarding:

The households of an economy may have hoarded some money from their past income. This is called idle saving or hoarding. If the households spend money at present from their idle saving, then this is called dishoarding. People hoard money because they like to hold idle cash.

They convert these idle savings into loanable funds when they see that the rate of interest (r) rises. The more the rate of interest rises, the more would be the amount of dishoarding. Therefore, dishoarding (DH) is an increasing function of r. That is why the DH curve would be a positively sloped curve like the one shown in Fig. 17.2. This curve tells us what would be the amount of DH at any r.

(iii) Bank Money:

The commercial banks also supply loanable funds. These banks create credit money when they give loans to business. The creation of credit money by the banks is another source of loanable funds.

The bank-created-money, or the bank money (BM) as it is called, is an increasing function of r. That is why the BM curve in Fig. 17.2 has been a posi­tively sloped curve. We can know from this curve what the amount of BM is at any particular r.

(iv) Dis-Investment:

Generally, the industries of a country build up their reserve funds to make up for the depreciation of the capital goods. When need arises an industry replaces its capital goods by spending money from its reserve fund. Now, if recession continues in any industry, its entrepreneurs do not wish to replace the depreciated capital goods, they decide to leave the industry.

Therefore, they now convert their reserve funds into loanable funds. This conversion of funds reserved for the replacement of fixed capital goods into loanable funds is called disinvestment (DI).

Since these funds are now used to earn interest income, the higher the r, the higher would be the amount of DI, i.e., DI would be an increasing function of r, and the DI curve like the one shown in Fig. 17.2 would be upward sloping. From this curve, we come to know what would be the amount of DI at any r.

From the above discussion, it follows that the total supply of loanable funds (SL) at any particular rate of interest will be

SL = s(r) + DH(r) + BM(r) + DI(r) = SL(r)                             (17.5)

(17.5) gives us that SL is a function of r.

Since each component of SL is an increasing function of r, SL would also be an increasing function of r. As defined in eqn. (17.5), the SL curve would be a horizontal summation of the curves for its components like S, DH, etc., and the SL curve—like all its component curves— would be upward sloping as has been shown in Fig. 17.2.

Demand for Loanable Funds:

The factors that determine the demand for loanable funds are:

(i) Investment Demand:

The demand for loans for investment purposes is an important source of demand for loanable funds. The business firms demand loans for buying capital goods. Investment demand for loans (i) is a decreasing function of the rate of interest (r).

That is, if r rises or falls, i falls or rises, respectively. This is because, according to the loanable funds theory, investment demand for loans (i) depends on the marginal product (MP) of capital. Owing to the law of diminishing returns, the more the use of capital, the less is the MP of capital.

That is why the firms would increase their use of capital, i.e., they would demand more of loans for having more of capital goods when the rate of interest diminishes. For, if r diminishes, then only the fall in the marginal product of capital would be balanced by the fall in the interest expenses or the cost of capital.

On the other hand, if r increases, the firms would reduce the investment demand for loans. Therefore, i is a decreasing function of r. That is why, the i curve in Fig. 17.2 has been negatively sloped.

(ii) Consumption Demand:

Another source of demand for loans is needs of consump­tion. Quite often the households demand loans for buying durable consumer goods like house, motor car, refrigerator, air-conditioner, etc. We may call this demand for loans con­sumption demand (CD). As r rises or falls, CD falls or rises, i.e., CD is a decreasing func­tion of r. That is why the CD curve in Fig. 17.2 has been shown to be sloping downward towards right.

(iii) Demand for Hoarding:

The money that the households save may be converted into loanable funds if they keep the money in banks, or in insurance companies through pay­ment of premiums, or if they buy bonds with the money, or if they keep the money in some other financial institutions. But, instead of doing this, they sometimes keep a portion of the money with themselves in the form of cash, i.e., they hoard a portion of their savings.

The savings then become idle. Here the households demand a portion of their saved money for hoarding. Now, the demand for hoarding (H) is a decreasing function of r.

For, as r rises, more of savings is kept in financial institutions to obtain interest at higher rates and H becomes less; on the other hand, as r falls, H increases, for now, conversion of savings into loanable funds is discouraged. That is why the H curve in Fig. 17.2 is sloping downward towards right.

There is another way in which there may be a demand for loanable funds for holding idle savings. Sometimes the households do not lend all the money they receive by selling bonds and financial instruments—a part of the money obtained by them is held as idle savings or hoard­ing. Here also the demand for hoarding (H) depends upon r. The higher the r, the more would be the amount of this H.

Therefore, the H curve in its totality would be sloping downward towards right like the one shown in Fig. 17.2. We can know from this H curve what would be H at any particular rate of interest.

From the discussion above, it is obvious that the total demand for loanable funds (DL) at any r would be

DL = i(r) + CD(r) + H(r) = DL(r)                                        (17.6)

(17.6) gives us that DL is a function of r. Since each component of DL is a decreasing function of r, DL also would be a decreasing function of r. As defined in eqn. (17.6), the DL curve, like the SL curve, would be a horizontal summation of the curves for its components like i, CD, etc., and the DL curve, like all its component curves, would be sloping downward to­wards right as has been shown in Fig. 17.2.

Determination of the Rate of Interest:

According to the loanable funds theory, the rate of interest at which the demand for and supply of loanable funds are equal is the equilibrium rate at which the market for loanable funds would be in equilibrium. Therefore, the condition for equilibrium rate of interest here is

i + H + CD = s + BM + DH + DI                                           (17.7)

That is, the equilibrium r will be determined at the point of intersection E of the DL and SL curves in Fig. 17.2. This equilibrium r is r₀, and the equilibrium DL = SL value is DL₀ = SL₀. That is, at the equilibrium r = r₀, the demand for and supply of loanable funds have been equal to each other.

It is also seen in Fig. 17.2 that at r < r₀, we have DL > SL. Consequently, in the perfectly competitive loan market, r would increase owing to pressure of excess demand for loanable funds till, at r = r₀, DL falls to the level of SL. On the other hand, at r > r₀, we have SL > DL. As a result, r would fall owing to the pressure of excess supply of loanable funds, till, at r = r₀, SL falls to the level of DL.

Therefore, that if the rate of interest in the market for loanable funds be less than or more than the equilibrium rate, then the behaviour of the people that supply and demand loanable funds would ensure that the market comes back to equilibrium. That is why the demand- supply equilibrium in the market for loanable funds is considered to be a stable equilibrium.

Critical Estimate:

The neoclassical or the loanable funds theory of interest rate determination is more comprehen­sive than the classical theory. For the classical theory only considers the real factors determin­ing the demand for and supply of capital whereas the loanable funds theory not only considers the real factors but also considers the monetary factors like money demand for idle savings, supply of bank money and supply of money due to dishoarding.

However, although more comprehensive than the classical theory, the loanable funds theory is also an incomplete theory like the classical theory. For, like the classical theory, here also, it has been assumed that saving is an increasing function of the rate of interest only. But, accord­ing to Keynes, saving is more of an increasing function of income (y) than it is an increasing function of the rate of interest (r).

Therefore, as in the case of the classical theory, in the loanable funds theory also, if we are to know the position of the s(r) function, we have to know y. Since the position of the s(r) function determines the position of SL(r) function, in order to know the position of the latter function also, we have to know y.

Therefore, as the matter stands, unless we know y, we cannot know the position of the SL(r) function or curve and, therefore, we cannot know what is the point of intersection of the DL(r) and the SL(r) curves and what is (equilibrium) r at that point.

In other words, in order to obtain (equilibrium) r, we have to know y.

However, from the theory of investment multiplier, we know that investment (i) via multi­plier determines y and we also have known that i depends on r, since i = i (r). Thus, we have obtained: if we know r, we can know i; if we know i, we can know y; and if we know y, we can know (equilibrium) r.

That is, in the loanable funds theory, like the classical theory of interest, r is determined only when r is known beforehand. Therefore, the loanable funds theory also cannot determine the rate of interest—the theory is indeterminate.

Lastly, we have to note another point also. For the income level of a country to be in equilibrium, we should have s(r) = i(r), and this latter condition is satisfied in the classical theory at the equilibrium r.

But in the loanable funds theory, at the equilibrium r (17.7) is satisfied, but satisfaction of (17.7) does not guarantee s(r) = i(r) or the equilibrium level of income, i.e., here, at the equilibrium r, y may be changing, leading to changes in the position of the SL(r) function as also changes in the position of the point of intersection of the DL(r) and SL(r) functions as also changes in equilibrium r. In this respect also, r cannot be deter­mined in the loanable funds theory.