Externalities and Social Welfare (With Diagram)

Externalities and Social Welfare!

Subject-Matter of Externalities and Social Welfare:

We know that perfect competition leads to a Pareto-optimal general equilibrium.

We also assumed together with usual assumptions of perfect competition that there were no externalities of production and consumption. We first explain the nature of externalities and then show how they prevent the attainment of a Pareto-optimal position by leading to divergences between private and social costs and benefits.

We assume that the firms contribute to the development of the local communities’ recreational facilities, such as parks and schools, in order to improve the overall living conditions and output of their work force. If these facilities are available to the general public there will be divergence between the private marginal benefits (PMB) and the social marginal benefits (SMB).

This difference is called a favourable externality of production.

Now consider an unfavorable externality of production that may result from the expansion of an industry, namely, smoke nuisance. Suppose that, as the industry grows, the air becomes increasingly polluted with smoke from the factory chimneys.

People in the community not only suffer discomfort because of the smoke, but also pay higher cleaning and laundry bills. In terms of social welfare, we must take into account these additional costs, in which case MSC > MPC.

There are also consumption externalities which distort the social optimum. A favourable consumption externality would occur if the consumption pattern of an individual results in benefits to others. For example, if it is worth for me to put money into a public record player to hear a record, the SMB > PMB to the extent that other people enjoy at my expenditure.

This indicates that the overall benefit derived from the expenditure is underestimated. And an unfavorable externality of consumption would occur if I decide to try out my new power lawn mower at seven o’clock Sunday morning and disturb my sleeping neighbors.

The term ‘market failure’ refers to the failure of perfectly competitive markets to attain a Pareto optimality because of externalities. The market failure occurs because the market does not automatically charge prices to the external effects of using the resources.

A good example is air pollution. People may have to pay higher costs because of pollution which the market does not take into account. Thus, there is a divergence between private costs and social costs.

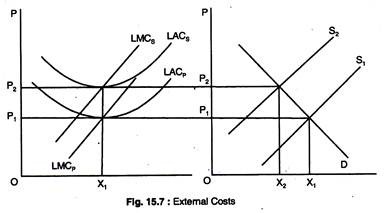
Fig. 15.7 shows a competitive firm and industry. If only private costs are taken into account, the industry will be in long-run equilibrium when the P = (minimum point) LAC at output X₁ and price P₁. Now, suppose all the external costs were somehow included in the firm’s cost curves. If this is done, LAC_P (private costs) would rise to LAC_S (social costs, private and external).

Now minimum LAC_S > P₁ which means some firms will leave the industry and the industry supply curve shift to the left. When the supply curve shifts to S₂ and the price to P₂ – minimum point on LAC_S and the industry once again is in equilibrium. Thus, if the external costs are included, then the price would be higher and less goods would be produced and sold and less pollution would be generated.

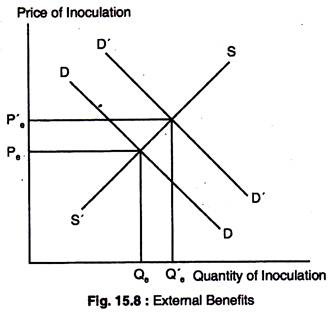
We will demonstrate external benefits in Fig. 15.8. Positive classic example of positive externality is that even when people do not receive inoculations against polio, small pox, etc. benefits from everyone else being inoculated, for epidemics will not break out. Thus, there are benefits that are external to each individual’s decision to be inoculated.

In Fig. 15.8, we show the demand curve, without external benefits as DD and the supply curve as SS. The equilibrium quantity is Q_e and the price, P. We assume that inoculation against contagious diseases generate external benefits to those individuals who may not be inoculated but who benefit because epidemics will not break out.

If such external benefits are taken into account, the demand curve would shift out from DD to D’D’. The new equilibrium quantity would be Q’_e and new equilibrium price would be P’_e. Without corrective action, this society is not devoting enough resources to inoculations against diseases.

Summary of Externalities:

We have seen that when there are external costs, the market will tend to over allocate resources to the production of the good in question. On the other hand, when there are external benefits, the market forces will under-allocate resources for the production of that good.

When there is over or under-allocation of resources to the production of goods or services of externalities, we call these cases of market failure. The price system or market fails to present the correct signals to the participants.

Public good externalities stem from the peculiar nature of a public good. A public good is a good such that any individual’s consumption of the good does not reduce the amount of the good available to any other consumer. For example, national defence system that protects me also protects any other members of the society.

Thus, the marginal social cost of making the good available to one more individual is zero. But the social benefit increases as more people consume the public good. Hence, the MSB and the MSC and thus Pareto-optimality is not attained.

Compensating Criteria of Social Welfare:

In the absence of a social welfare function, how do we evaluate the welfare effect of a redistribution of income that makes some people better-off and others worse-off? Many governments’ policies lead to a change in the distribution of income, such as social security benefits, various forms of taxes, etc. The problem is to determine whether or not redistribution results in a net gain in social welfare.

To deal with this problem, economists developed what is-known as compensation principles. These principles (criteria) hold that an income redistribution — or any other social change — would result in a gain in welfare if those who gain from the change are able to fully compensate those who lose, and still feel better-off. For example, suppose that a change causes A to feel that he has gained £ 100, whereas B has lost £60.

According to Kaldor criterion, this change represents a net gain even if actual payment has not been made. A could pay B £60 and still remain better- off by £40. Unfortunately, if the compensation has not been actually made and A keeps his full gain of £100, there still may not be a net gain, since it is possible that B’s non-receipt of £60 may cause hardship to him that outweighs all A’ gain.

The only way to avoid this problem is to assume an equal marginal utility of money for A and B, but this involves interpersonal utility comparisons, which we wish to avoid.

Scitovsky pointed out the problem associated with Kaldor’s compensation criterion. He mentioned that if the compensation payment is not actually made, then, there is the possibility that, after the change occurs, a return to the original situation may also represent a net gain in terms of Kaldor criterion.

Thus, Scitovsky criterion suggests that not only must those who gain be able to compensate those who lose, but after the change is made, it must be impossible to do the reverse in order to return to the original situation. Although this test eliminates a source of possible Kaldor paradox, it is still open to the same criticism made in connection with the Kaldor approach.

Instead of Kaldor’s potential compensation we assume that compensation will actually be paid. If we make this assumption, we are, in effect, back to Pareto’s criterion, but with problems.

In order to compensate losers we must know the utility schedules of all the losses otherwise we would run into difficulties an individual might not know in advance how a given change would affect him, since they may be able to evaluate, or may not be aware, until well after the change has occurred.

In actual practice, losers may overstate their losses or losses may be claimed where no losses have been incurred. Finally, any compensation system would require a costly administrative machinery.

Output Efficiency:

For an economy to be efficient, it must not only produce goods at minimum cost, it must also produce combinations of goods that match people’s willingness to pay for them. As we know that the MRS of Y for X measures the consumer’s willingness to pay for an additional unit of X in terms of consuming less of Y. But the MRT measures the cost of an additional unit of X in terms of producing less Y.

An economy produces output efficiently only if, for each consumer, the following condition is satisfied:

MRS = MRT………(4)

This condition is necessary for efficiency, because if the MRT equals 1, but the MRS equals 2, in such a situation, consumers are willing to give up 2 units of Y to get 1 unit of X, but the cost of getting the additional X is only 1 unit of Y.

Clearly, not enough X is being produced. To achieve efficiency, production of X must be increased, so that, the MRS falls and the Morrises, until the two are equal. The outcome is efficient only when MRS = MRT for all pairs of goods.

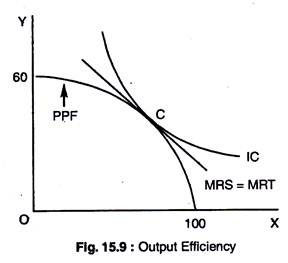
Fig. 15.9 shows this efficiency condition. Here, we have superimposed one consumer’s indifference curve on the production possibilities frontier from Fig. 15.3. We note that C is the only point on the PPF that maximises the consumer’s satisfaction, because, at this point of tangency of the indifference curve and the PPF, the MRS (the slope of the IQ and the MRT (the slope of the production frontier) are equal.

If we are planners of an economy, we would face a difficult problem.

To achieve efficiency we must equate the MRT with the MRS of the consumer. But if different consumers have different preferences for X and Y, how can we decide what levels of X and Y to produce and what amount to give to every consumer, so that all consumers have the same MRS? The logistical and informational costs of doing this are enormous. However, a well-functioning competitive market can achieve the same efficient outcome at a low cost.