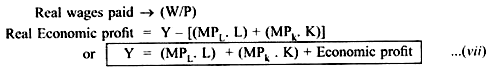The Marginal Product and Product Function of Labors

The firms will choose that amount of the factor that will maximize its profit.

How much labour to hire and capital to rent will depend on the marginal productivity (MP) of the factor.

MP is the addition to the total output brought by the employment of an additional unit of factor of production.

As the firm increases the factor, MP of that factor decreases.

MP_L = f(K, L + 1) – f(K, L)

Similarly,

MP_k = f(K + 1, L) – f(K, L)

where,

(K + 1) → additional unit of capital used.

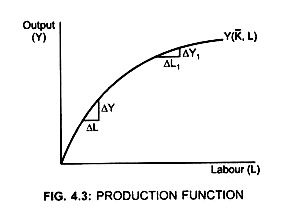
Slope of production function is represented by MP_L.

Since MP_L decreases with increase in the employment of labour, (with capital constant), the slope of production function decreases. Thus, the production function becomes flatter.

As output increases at decreasing rate due to fall in MP of labour, the firm is willing to hire more labour only at a less price (wage).

Before employing an additional labour, the firm will compare extra revenue (∆R) received from increase in production with the extra cost (∆C) incurred on hiring an additional labour (that is, wages).

Increase in revenue depends on:

1. MP of labour (MP_L)

2. Price of output (P)

.^.. ∆R = MP_L.P

Firm will hire labour till: ∆R = wages paid (W)

or

MP_L .P = W

or

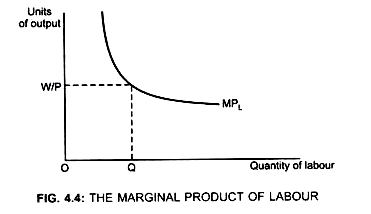
MP_L = W/P Where: W/P → Real wage

Thus, it implies firm will hire the labour till the point where MP_L = Real wage.

Algebraically:

Change in profit (∆π) from hiring additional labour:

Thus, when each factor is paid according to its marginal productivity the firm will maximize its profit. This is achieved when it hires OQ labour (Figure. 4.4)

Thus, equation (vii) shows, National income (Y) is divided among:

1. Labour in form of wages.

2. Capital in form of interest.

3. Economic Profit.