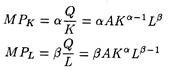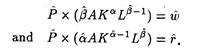Profit-Maximizing Levels of Input Usage | Economics

In this article we will discuss about the Profit-Maximizing Levels of Input Usage.

A firm can also reach the point of profit-maximization through selection of the optimal level of employment of its inputs. In other words, a firm can maximise profits by selecting the optimal value for either output or input usage.

To start with, we look at the case of a single variable input. Later, we shall look at a more complex situation involving several variable inputs.

One Variable Input:

Suppose the only variable input is labour. Recall that the firm will maximise profit if it employs labour at the level at which the value of the marginal product of labour equals the market wage rate:

VMP_L = w

For a firm in a competitive market, VMP_L is equal to the price of the firm’s output times the marginal physical product of labour. The wage rate is market determined; so an individual firm accepts the going wage rate in making its input purchase decision.

Therefore, to implement this decision, the firm receives three types of information:

(1) The market wage rate,

(2) The price of its output, and

(3) The marginal product function for labour.

We know how the first two are determined. Hence, the only potential difficulty is in finding the marginal product function for labour.

It has expressed a production function with a single variable input as Q = ƒ(L).

An appropriate statistical production function would be a log-linear function

Q = AL^β

where 0 < β < 1. With this short-run production function, the marginal product function for labour is

Once we have obtained the price forecast for the firm’s output (P), the forecasted wage rate (w), and estimates of the parameters of the production function (β and  ), we can express the profit- maximizing condition as

P̂ x β̂ÂL^β̂-1 =  ŵ

To arrive at the profit-maximizing employment level for labour, we then need to solve this equation for L.

Several Variable Inputs:

If the firm hires several variable factors, the computation becomes more complex.

Now suppose the firm’ uses two variable inputs — capital and labour. The profit-maximization conditions require that the value of the marginal products for the inputs be equal to the respective input prices. That is,

P x MP_L = w and P x MP_K= r

where r is the user cost of capital, i.e., the cost to the firm of using a unit of capital (also known as the market rate of interest).

We have already examined how the firm can obtain its price forecast (P). And the firm can obtain forecasts of the price of capital (r) in much the same way it obtains forecasts for the wage rate (w). Hence, the remaining part of the exercise is concerned with the determination of the marginal product functions for labour and capital.

In the case of a two-input production function, Q =ƒ (K,L), we can use the Cobb-Douglas production function:

Q = AK^α L^β

where 0 < α, β < 1. Recall that with this production function, the marginal product functions are

After estimating the production function (i.e., we have the statistical estimates of A, a and (3) we can use it together with the forecasts of the output price and the prices of inputs and then express the two profit-maximizing conditions in the following form:

To determine the profit-maximizing levels of wage and interest, we need to solve these two equations simultaneously for L and K.