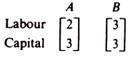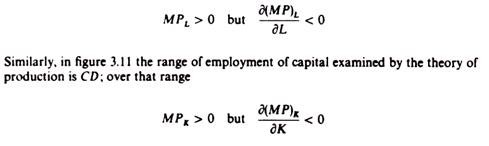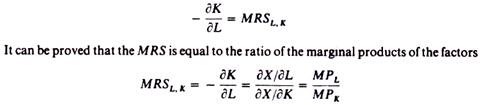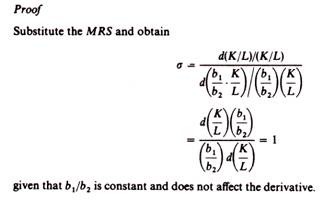The Production Function for a Single Product

The production function is a purely technical relation which connects factor inputs and outputs.

It describes the laws of proportion, that is, the transformation of factor inputs into products (outputs) at any particular time period.

The production function represents the technology of a firm of an industry, or of the economy as a whole.

The production function includes all the technically efficient methods or production. A method of production (process, activity) is a combination of factor inputs required for the production of one unit of output. Usually a commodity may be produced by various methods of production.

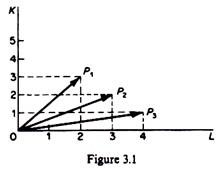
For example, a unit of commodity x may be produced by the following processes:

Activities may be presented graphically by the length of lines from the origin to the point determined by the labour and capital inputs. The three processes above are shown in figure 3.1. A method of production A is technically efficient relative to any other method B, if A uses less of at least one factor and no more from the other factors as compared with B.

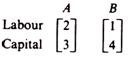
For example, commodity y can be produced by two methods:

Method B is technically inefficient as compared with A. The basic theory of production concentrates only on efficient methods. Inefficient methods will not be used by rational entrepreneurs. If a process A uses less of some factor(s) and more of some other(s) as compared with any other process B, then A and B cannot be directly compared on the criterion of technical efficiency.

For example, the activities are not directly comparable. Both processes are considered as technically efficient and are included in the production function (the technology). Which one of them will be chosen at any particular time depends on the prices of factors. The theory of production describes the laws of production. The choice of any particular technique (among the set of technically efficient processes) is an economic one, based on prices, and not a technical one. We note here that a technically efficient method is not necessarily economically efficient. There is a difference between technical and economic efficiency.

An isoquant includes (is the locus of) all the technically efficient methods (or all the combinations of factors of production) for producing a given level of output. The production isoquant may assume various shapes depending on the degree of substitutability of factors.

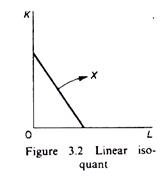
Linear isoquant:

This type assumes perfect substitutability of factors of production: a given commodity may be produced by using only capital, or only labour, or by an infinite combination of K and L (figure 3.2).

 Input-output isoquant:

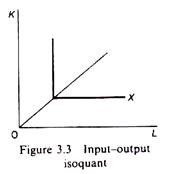
This assumes strict complementarity (that is, zero substitut­ability) of the factors of production. There is only one method of production for any one commodity. The isoquant takes the shape of a right angle (figure 3.3). This type of isoquant is also called ‘Leontief isoquant’ after Leontief, who invented the input- output analysis.

Kinked isoquant:

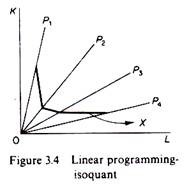
This assumes limited substitutability of K and L. There are only a few processes for producing any one commodity. Substitutability of the factors is possible only at the kinks (figure 3.4). This form is also called ‘activity analysis-iso- quant’ or ‘linear-programming isoquant’, because it is basically used in linear pro­gramming.

Smooth, convex isoquant:

This form assumes continuous substitutability of K and L only over a certain range, beyond which factors cannot substitute each other. The isoquant appears as a smooth curve convex to the origin (figure 3.5). 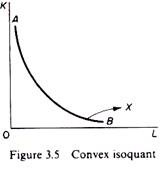It should be noted that the kinked isoquants are more realistic. Engineers, managers, and production executives consider the production processes as discrete rather than in a continuous array. However, traditional economic theory has mostly adopted the continuous isoquants, because they are mathematically simpler to handle by the simple rules of calculus.

We may consider the continuous isoquant as an approximation to the more realistic form of a kinked isoquant as we increase the number of processes the kinks come closer and closer, until at the limit (as the number of processes becomes infinite) the isoquant becomes a smooth curve.

The production function describes not only a single isoquant, but the whole array of isoquants, each of which shows a different level of output. It shows how output varies as the factor inputs change. Production functions involve (and can provide measurements of) concepts which are useful tools in all fields of economics.

The main concepts are:

1. The marginal productivity of the factors of production.

2. The marginal rate of substitution and the elasticity of substitution.

3. Factor intensity.

4. The efficiency of production.

5. The returns to scale.

The general mathematical form of the production function is

Y = f(L, K, R, S, v, y)

Where Y — output

L = labour input

K — capital input

R = raw materials

S = land input

v = returns to scale

y = efficiency parameter.

All variables are flows, that is, they are measured per unit of time. In its general form the production function is a purely technological relationship between quantities of inputs and quantities of output. Prices of factors or of the product do not enter into the produc­tion function. They are used only for the production decision of the firm or other economic entities.

However, in practice it has been observed that raw materials bear a constant relation to output at all levels of production. For example, the number of bricks for a given type of house is constant, irrespective of the number of houses built; similarly the metal required for a certain type of car is constant, irrespective of the number of cars produced. This allows the subtraction of the value of raw materials from the value of output, and the measurement of output in terms of value added (X)

X = Y – R

Of course, in this way we destroy the pure technological nature of the production func­tion, since the prices of raw materials and of the output are utilized: value added is measured, by necessity, in monetary units. The input of land, S, is constant for the economy as a whole, and hence does not enter into an aggregate production function. However, S is not constant for individual sectors or for individual firms. In these cases land-inputs are lumped together with machinery and equipment, in the factor K.

Thus the production function in traditional economic theory assumes the form

X = ƒ(L, K, v, y)

The factor v, ‘returns to scale’, refers to the long-run analysis of the laws of production, since it assumes change in the plant. The efficiency parameter, y, refers to the entrepreneurial-organisational aspects of production. Two firms with identical factor inputs (and the same returns to scale) may have different levels of output due to differences in their entrepreneurial and organisa­tional efficiency.

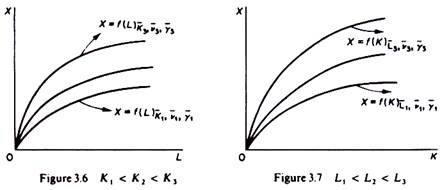
Graphically, the production function is usually presented as a curve on two-dimensional graphs. Changes of the relevant variables are shown either by movements along the curve that depicts the production function, or by shifts of this curve. The most commonly used diagrams for the production function of a single commodity are shown in figures 3.6 and 3.7. In figure 3.6 each curve shows the relation between X and L for given K, v and y. As labour increases, ceteris paribus, output increases: we move along the curve depicting the production function. If capital (and/or v, and/or y) increase, the production function X = f(L) shifts upwards.

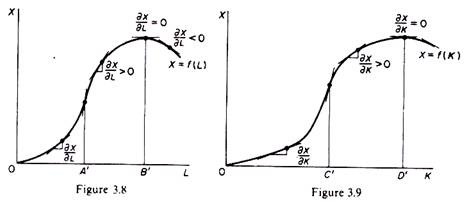
In figure 3.7 each curve shows the relation between X and K for given L, v and y. As capital increases, ceteris paribus, output increases: we move along the curve. If L (and/or v, and/or y) increase the production function X = ƒ (K) shifts upwards.

The slopes of the curves in figures 3.6 and 3.7 are the marginal products of the factors of production. The marginal product of a factor is defined as the change in output resul­ting from a (very small) change of this factor, keeping all other factors constant. Mathematically the marginal product of each factor is the partial derivative of the production function with respect to this factor. Thus

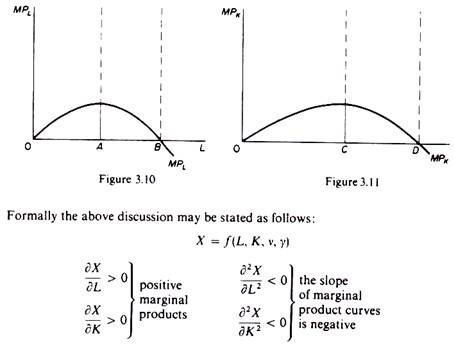
In principle the marginal product of a factor may assume any value, positive, zero or negative. However, basic production theory concentrates only on the efficient part of the production function, that is, on the range of output over which the marginal products of the factors are positive. No rational firm would employ labour beyond OB, or capital beyond 0D, since an increase in the factors beyond these levels would result in the reduction of the total output of the firm. Ranges of output over which the marginal products of the factors would be negative (ranges beyond OB’ in figure 3.8, and 0D’ in figure 3.9) imply irrational behaviour of the firm, and are not considered by the theory of production.

Furthermore, the basic theory of production usually concentrates on the range of output over which the marginal products of factors, although positive, decrease, that is, over the range of diminishing (but non-negative) productivity of the factors of pro­duction: the ranges of output considered by the traditional theory are A’B’ in figure 3.8 and CD’ in figure 3.9. These ranges of output have been shown in figures 3.6 and 3.7.

Alternatively we may say that the theory of production concentrates on levels of employment of the factors over which their marginal products are positive but decrease: in figure 3.10 the range of employment of L examined by the theory of production is AB; over that range

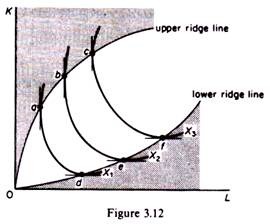
These conditions imply that the traditional theory of production concentrates on the range of isoquants over which their slope is negative and convex to the origin. In figure 3.12 the production function is depicted in the form of a set of isoquants. By construction the higher to the right an isoquant, the higher the level of output it depicts.

Clearly isoquants cannot intersect, by their construction. We said that traditional economic theory concentrates on efficient ranges of output, that is, ranges over which the marginal products of factors are diminishing but positive. The locus of points of iso­quants where the marginal products of the factors are zero form the ridge lines.

The upper ridge line implies that the MP of capital is zero. The lower ridge line implies that the MP of labour is zero. Production techniques are only (technically) efficient inside the ridge lines. Outside the ridge lines the marginal products of factors are negative and the methods of production are inefficient, since they require more quantity of both factors for producing a given level of output.

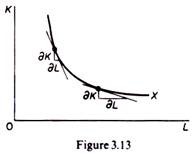
Such inefficient methods are not considered by the theory of production, since they imply irrational behaviour of the firm. The condition of positive but declining marginal products of the factors defines the range of efficient production (the range of isoquants over which they are convex to the origin). The slope of the isoquant (— K/L) defines the degree of substitutability of the factors of production (figure 3.13).

The slope of the isoquant decreases (in absolute terms) as we move downwards along the isoquant, showing the increasing difficulty in substituting K for L. The slope of the isoquant is called the rate of technical substitution, or the marginal rate of substitution (MRS) of the factors

Proof:

The slope of a curve is the slope of the tangent at any point of the curve. The slope of the tangent is defined by the total differential. In the case of the isoquant the total differential is the total change in X resulting from small changes in both factors K and L. Clearly if we change K by K, the output X will change by the product K times the marginal product of capital

The marginal rate of substitution as a measure of the degree of substitutability of factors has a serious defect: it depends on the units of measurement of the factors. A better measure of the ease of factor substitution is provided by the elasticity of sub­stitution. The elasticity of substitution is defined as the percentage change in the capital labour ratio, divided by the percentage change in the rate of technical substitution

The elasticity of substitution is a pure number independent of the units of measurement of K and L, since both the numerator and the denominator are measured in the same units.

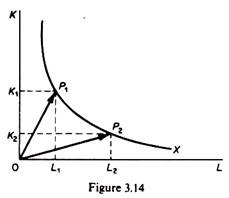
The factor intensity of any process is measured by the slope of the line through the origin representing the particular process. Thus the factor intensity is the capital-labour ratio. In figure 3.14 process P₁ is more capital intensive than process P₂. Clearly

K₁ / L₁ > K₂ / L₂

The upper part of the isoquant includes more capital-intensive processes. The lower part of the isoquant includes more labour-intensive techniques.

Example

Let us illustrate the above concepts with a specific form of production function, namely the Cobb-Douglas production function. This form is the most popular in applied research, because it is easiest to handle mathematically.

4. Factor intensity. In a Cobb-Douglas function factor intensity is measured by the ratio b₁/b₂. The higher this ratio the more labour intensive the technique. Similarly the lower the ratio b₁/b₂ the more capital intensive the technique.

5. The efficiency of production. The efficiency in the organisation of the factors of production is measured by the coefficient b₀. Intuitively it is clear that if two firms have the same K, L, b₁ and b₂ and still produce different quantities of output, the differ­ence can be due to the superior organisation and entrepreneurship of one of the firms, which results in different efficiencies. The more efficient firm will have a larger b₀ than the less efficient one.

6. The returns to scale. This concept will be developed in the next section, since it refers to the long-run analysis of production. We state here that in a Cobb-Douglas function the returns to scale are measured by the sum of the coefficients b₁ + b₂.