‘Time value of money’ is central to the concept of finance. It recognizes that the value of money is different at different points of time. Since money can be put to productive use, its value is different depending upon when it is received or paid.
In simpler terms, the value of a certain amount of money today is more valuable than its value tomorrow. It is not because of the uncertainty involved with time but purely on account of timing. The difference in the value of money today and tomorrow is referred to as the time value of money.
1. Meaning of Time Value of Money
The time value of money is one of the basic theories of financial management, it states that ‘the value of money you have now is greater than a reliable promise to receive the same amount of money at a future date’.
The time value of money (TVM) is the idea that money available at the present time is worth more than the same amount in the future due to its potential earning capacity. This core principle of finance holds that, provided money can earn interest, any amount of money is worth more the sooner it is received.
ADVERTISEMENTS:
The time value of money is the greater benefit of receiving money now rather than receiving later. It is founded on time preference. The principle of the time value of money explains why interest is paid or earned? Interest, whether it is on a bank deposit or debt, compensates the depositor or lender for the time value of money.
2. Concept of Time Value of Money
Important terms or concepts used in computing the time value of money are-
(1) Cash-flow
(2) Cash inflow
ADVERTISEMENTS:
(3) Cash outflow
(4) Discounted Cash flow
(5) Even cash flows /Annuity cash flows
(6) Uneven/mixed streams of cash flows
ADVERTISEMENTS:
(7) Single cash flows
(8) Multiple cash flows
(9) Future value
(10) Present value
(11) Compounding
(12) Discounting
(13) Effective interest rate / Time preference rate
(14) Risks and types of risks
(15) Uncertainty, and
ADVERTISEMENTS:
(16) Doubling Period.
The above concepts are briefly explained below:
(1) Cash-Flow:
Cash flow is either a single sum or the series of receipts or payments occurring over a specified period of time. Cash flows are of two types namely, cash inflow and cash outflow and cash flow may be of much variety namely; single cash flow, mixed cash flow streams, even cash flows or uneven cash flows.
ADVERTISEMENTS:
(2) Cash Inflow:
Cash inflows refer to the receipts of cash, for the investment made on the asset/project, which comes into the hands of an individual or into the business organisation account at a point of time/s. Cash inflow may be a single sum or series of sums (even or uneven/mixed) over a period of time.
(3) Cash Outflow:
Cash outflow is just opposite to cash inflow, which is the original investment made on the project or the asset, which results in the payment/s made towards the acquisition of asset or getting the project over a period of time/s.
ADVERTISEMENTS:
(4) Discounted Cash Flow- The Mechanics of Time Value:
The present value of a future cash flow (inflows or outflows) is the amount of current cash that is of equivalent value to the decision maker today. The process of determining present value of a future payment (or receipts) or a series of future payments (or receipts) is called discounting. The compound interest rate used for discounting cash flows is called discount rate.
(5) Even Cash Flows /Annuity Cash Flows:
Even cash flows, also known as annuities, are the existence of equal/even/fixed streams of cash flows may be a cash inflow or outflow over a specified period of time, which exists from the beginning of the year.
Annuities are also defined as ‘a series of uniform receipts or payments occurring over a number of years, which results from an initial deposit.’
In simple words, constant periodic sums are called annuities.
ADVERTISEMENTS:
Annuity Aspects:
It is essential to discuss some of the aspects related to annuities, which are discussed as below:
1. Annuitant
2. Status
3. Perpetuity
4. Various types of Annuity-
ADVERTISEMENTS:
i. Annuity Certain
ii. Annuity Contingent
iii. Immediate or Ordinary annuity
iv. Annuity due
v. Perpetual annuity
vi. Deferred annuity
ADVERTISEMENTS:
5. Annuity factor-
(i) Present Value Annuity factor, and
(ii) Compound value annuity factor.
A brief description each of the above aspects is as follows:
i. Annuitant is a person or an institution, who receives the annuity.
ii. Status refers to the period for which the annuity is payable or receivable.
ADVERTISEMENTS:
iii. Perpetuity is an infinite or indefinite period for which the amount exists.
iv. a. Annuity Certain refers to an annuity which is payable or receivable for a fixed number of years.
b. Annuity Contingent refers to the payment/receipt of an annuity till the happening of a certain event/incident.
c. Immediate annuities are those receipts or payments, which are made at the end of the each period.
d. A series of cash flows (i.e., receipts or payments) starting at the beginning of each period for a specified number of periods is called an Annuity due. This implies that the first cash flow has occurred today.
e. Perpetual annuities when, annuities payments are made for ever or for an indefinite or infinite periods.
f. Deferred annuities are those receipts or payments, which starts after a certain number of years.
v. (a) Present Value of Annuity factor is the sum of the present value of Re. 1 for the given period of time duration at the given rate of interest;
(b) Compound value/Future value of annuity factor is the sum of the future value of Re. 1 for the given period of time duration at the given rate of interest. This is the reciprocal of the present value annuity discount factor.
Note – When the interest rate rises, the present value of a lump sum or an annuity declines. The present value factor declines with higher interest rate, other things remaining the same.
vi. Sinking fund is a fund which is created out of fixed payments each period (annuities) to accumulate to a future some after a specified period. The compound value of an annuity can be used to calculate an annuity to be deposited to a sinking fund for ‘n’ period at ‘i’ rate of interest to accumulate to a given sum.
(6) Uneven/Mixed Streams of Cash Flows:
Uneven cash flows, as the concept itself states, is the existence of un-equal or mixed streams of cash inflows emanating from the investment made on the assets or the project.
(7) Single Cash Inflows:
A single cash inflow is a single sum of receipt of cash generated from the project during the given period, for which the present value is ascertained by multiplying the cash inflow by the discount factor.
(8) Multiple Cash Inflows:
Multiple cash inflows (even or mixed cash inflows) are the series of cash flows, may be annuities/mixed streams of cash inflows which are generated from the project over the entire life of the asset.
(9) Future Value/Compound Value [FV/CV]:
The future value concept states as to how much is the value of current cash flow or streams of cash flows at the end of specified time periods at a given discount rate or interest rate. Future value refers to the worth of the current sum or series of cash flows invested or lent at a specified rate of return or rate of interest at the end of specified period.
In simple terms, future value refers to the value of a cash flow or series of cash flows at some specified future time at specified time preference rate for money.
(10) Compounding:
The process of determining the future value of present money is called compounding. In other words, compounding is a process of investing money, reinvesting the interest earned & finding value at the end of specified period is called compounding.
In simple words, calculation of maturity value of an investment from the amount of investment made is called compounding.
Under compounding technique the interest earned on the initial principal become part of principal at the end of compounding period. Since interest goes on earning interest over the life of the asset, this technique of time value of money is also known as ‘compounding’.
The simple formula to calculate Compound Value in different interest time periods is-
(a) If Interest is added at the end of each year or compounded annually-
FV or CV = PV (1 + i)n
Where, FV or CV = Future Value or Compound Value, PV= Present Value,
(1 + i)n = Compound Value factor of Re.1 at a given interest rate for a certain number of years.
(b) If Interest is added/computed semi-annually and other compounding periods/multi- compounding-

Say for example;
(i) When Compounding is made semi-annually, then m=2 (because two half years in one year).
(ii) When Compounding is made quarterly, then m= 4 (because, 4 quarter years in one year).
(iii) When Compounding is made monthly, then m= 12 (because, 12 months in one year).
(11) Present Value:
The present value is just opposite to the future value. Present value refers to the present worth of a future sum of money or streams of cash flows at a specified interest rate or rate of return. It is also called a discounted value.
In simple terms it refers to the current value of a future cash flow or series of cash flows.
(12) Discounting:
The inverse of the compounding process is discounting technique. The process of determining the present value of future cash flows is called discounting.
Discounting or Present Value technique is more popular than compounding technique, since every individual or an organisation intends to have/hold present sums, rather than getting some amount of money after some time, because of time preference for money.


(13) Effective Interest Rate / Time Preference Rate:
Time preference rate is used to translate the different amounts received at different time periods; to amounts equivalent in value to the firm/individual in the present at common point reference. This time preference rate is normally expressed in ‘percent’ to find out the value of money at present or in future.
(14) Risk:
In business, the finance manager is supposed to take number of decisions under different situations. In all such decisions, there is an existence of risk and uncertainty.
Risk is the ‘variability of returns’ or the ‘chance of financial losses’ associated with the given asset. Assets that are having higher chances of loss or the higher rate of variability in returns are viewed as ‘risky assets’ and vice versa. Hence care should be taken to recognize and to measure the extent of risk associated with the assets, before taking the decision to invest on such risky assets.
3. Importance of Time Value of Money
The Consideration of time is important and its adjustment in financial decision making is also equally important and inevitable. Most financial decisions, such as the procurement of funds, purchase of assets, maintenance of liquidity and distribution of profits etc., affect the firm’s cash flows/movement of cash in and out of the organization in different time periods.
Cash flows occurring in different time periods are not comparable, but they should be properly measurable. Hence, it is required to adjust the cash flows for their differences in timing and risk. The value of cash flows to a common time point should be calculated.
To maximize the owner’s equity, it’s extremely vital to consider the timing and risk of cash flows. The choice of the risk adjusted discount rate (interest rate) is important for calculating the present value of cash flows.
For instance, if the time preference rate is 10 percent, it implies that an investor can accept receiving Rs.1000 if he is offered Rs.1100 after one year. Rs.1100 is the future value of Rs.1000 today at 10% interest rate.
Thus, the individual is indifferent between Rs.1000 and Rs.1100 a year from now as he/she considers these two amounts equivalent in value. You can also say that Rs.1000 today is the present value of Rs.1100 after a year at 10% interest rate.
Time value adjustment is important for both short-term and long-term decisions. If the amounts involved are very large, time value adjustment even for a short period will have significant implications.
However, other things being same, adjustment of time is relatively more important for financial decisions with long range implications than with short range implications. Present value of sums far in the future will be less than the present value of sums in the near future.
The concept of time value of money is of immense use in all financial decisions.
The time value concept is used
1. To compare the investment alternatives to judge the feasibility of proposals.
2. In choosing the best investment proposals to accept or to reject the proposal for investment.
3. In determining the interest rates, thereby solving the problems involving loans, mortgages, leases, savings and annuities.
4. To find the feasible time period to get back the original investment or to earn the expected rate of return.
5. Helps in wage and price fixation.
4. Reasons for Time Preference of Money / Reasons for Time Value of Money
There are three primary reasons for the time value of money- reinvestment opportunities; uncertainty and risk; preference for current consumption.
These reasons are explained below:
1. Reinvestment Opportunities:
The main fundamental reason for Time value of money is reinvestment opportunities.
Funds which are received early can be reinvested in order to earn money on them. The basic premise here is that the money which is received today can be deposited in a bank account so as to earn some return in terms of income.
In India saving bank rate is about 4% while fixed deposit rate is about 7% for one year deposit in public sector banks. Therefore even if the person does not have any other profitable investment opportunity to invest his funds, he can simply put his money in a savings bank account and earn interest income on it.
Let us assume that Mr. X receives Rs.100000 in cash today. He can invest or deposit this Rs.100000 in fixed deposit account and earn 7% interest p.a. Therefore at the end of one year his money of Rs.100000 grows to Rs.107000 without any efforts on the part of Mr. X.
If he deposits Rs.100000 in two years fixed deposit providing interest rate 7% p.a. then at the end of second year his money will grow to Rs.114490 (i.e. Rs.107000+ 7% of Rs.107000). Here we assume that interest is compounded annually i.e. we do not have a simple interest rate but compounded interest rate of 7%.
Thus Time value of money is the compensation for time.
2. Uncertainty and Risk:
Another reason for Time value of money is that funds which are received early resolves uncertainty and risk surmounting future cash flows. All of us know that the future is uncertain and unpredictable. At best we can make best guesses about the future with some probabilities that can be assigned to expected outcomes in the future.
Therefore given a choice between Rs.100 to be received today or Rs.100 to be received in future say one year later, every rational person will opt for Rs.100 today. This is because the future is uncertain. It is better to get money as early as possible rather than keep waiting for it.
The underlying principle is “A bird in hand is better than two in the bush.”
It must be noted that there is a difference between risk and uncertainty.
In a Risky situation we can assign probabilities to the expected outcomes. Probability is the chance of occurrence of an event or outcome. For example I may get Rs.100 with 90% probability in future. Therefore there is 10% probability of not getting it at all. In a risky situation outcomes are predictable with probabilities.
In case of an uncertain situation it is not possible to assign probabilities to the expected outcomes. In such a situation the outcomes are not predictable.
3. Preference for Current Consumption:
The third fundamental reason for Time value of money is preference for current consumption. Everybody prefers to spend money today on necessities or luxuries rather than in future, unless he is sure that in future he will get more money to spend.
Let us take an example, Your father gives you two options – to get Wagon R today on your 20th birthday OR to get Wagon R on your 21st birthday which is one year later.
Which one would you choose? Obviously you would prefer Wagon R today rather than one year later. So every rational person has a preference for current consumption. Those who save for future, do so to get higher money and hence higher consumption in future.
In the above example of a car if your father says that he can give you a bigger car, say Honda City on your 21st birthday, then you may opt for this option if you think that it is better to wait and get a bigger car next year rather than settling for a small car this year.
Thus we can say that the amount of money which is received early (or today) carries more value than the same amount of money which is received later (or in future). This is Time Value of Money.
5. Valuation Concepts
There are the following two valuation concepts:
1) Compound Value Concept (Future Value or Compounding)
2) Present Value Concept (Discounting)
1) Compound Value Concept:
The compound value concept is used to find out the Future Value (FV) of present money. A Future Value means that a given quantity of money today is worth more than what will be received at some point of time in future.
It is the same as the concept of compound interest, wherein the interest earned in a preceding year is reinvested at the prevailing rate of interest for the remaining period. Thus, the accumulated amount (principal + interest) at the end of a period becomes the principal amount for calculating the interest for the next period.

The compounding technique to find out the FV to present money can be explained with reference to:
i) The FV of a single present cash flow,
ii) The FV of a series of equal cash flows and
iii) The FV of multiple flows.
i) FV of a Single Present Cash Flow: The future value of a single cash flow is defined in term of equation as follows:

Illustration:
Mr. A makes a deposit of Rs. 10,000 in a bank which pays 10% interest compounded annually for 5 years. You are required to find out the amount to be received by him after 5 years.
Solution:
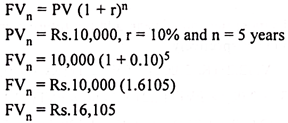
ii) Future Value of Series of Equal Cash Flows or Annuity of Cash Flows:
Quite often a decision may result in the occurrence of cash flows of the same amount every year for a number of years consecutively, instead of a single cash flow. For example, a deposit of Rs. 1,000 each year is to be made at the end of each of the next 3 years from today.
This may be referred to as an annuity of deposit of Rs. 1,000 for 3 years. An annuity is thus, a finite series of equal cash flows made at regular intervals.
In general terms, the future value of an annuity is given as:
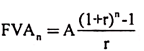

It is evident from the above that future value of an annuity depends upon three variables, A, r and n. The future value will vary if any of these three variables changes. For computation purposes, tables or calculators can be made use of.
Illustration:
Mr. A is required to pay five equal annual payments of Rs. 10,000 each in his deposit account that pays 10% interest per year. Find out the future value of annuity at the end of four years.
Solution:
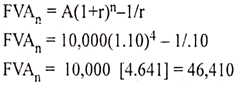
iii) Future Value of Multiple Flows:
Illustration:
Suppose the investment is Rs. 1,000 now (beginning of year 1), Rs.2,000 at the beginning of year 2 and Rs.3,000 at the beginning of year 3, how much will these flows accumulate at the end of year 3 at a rate of interest of 12 percent per annum?
Solution:
To determine the accumulated sum at the end of year, add the future compounded values of Rs. 1,000, Rs.2, 000 and Rs.3, 000 respectively:

2) Present Value Concept:
Present values allow us to place all the figures on a current footing so that comparisons may be made in terms of today’s rupees. Present value concept is the reverse of compounding technique and is known as the discounting technique.
As there are FVs of sums invested now, calculated as per the compounding techniques, there are also the present values of a cash flow scheduled to occur in future.
The present value is calculated by discounting technique by applying the following equation:
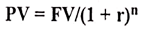
The discounting technique to find out the PV can be explained in terms of:
i) Present Value of a Future Sum:
The present value of a future sum will be worth less than the future sum because one forgoes the opportunity to invest and thus forgoes the opportunity to earn interest during that period. In order to find out the PV of future money, this opportunity cost of the money is to be deducted from the future money.
The present value of a single cash flow can be computed with the help of following formula:
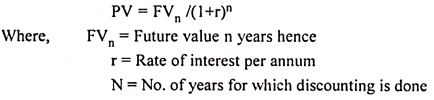
Illustration:
Find out the present value of Rs.3, 000 received after 10 years hence, if the discount rate is 10%.
Solution:
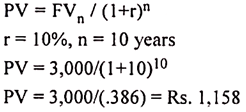
Illustration:
Mr. A makes a deposit of Rs. 5000 in a bank which pays 10% interest compounded annually. You are required to find out the amount to be received after 5 years.
Solution:
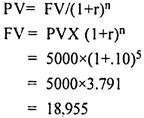
ii) PV of a Series of Equal Future Cash Flows or Annuity:
A decision taken today may result in a series of future cash flows of the same amount over a period of number of years.
For example, a service agency offers the following options for a 3-year contract:
a) Pay only Rs.2, 500 now and no more payment during next 3 years, or
b) Pay Rs.900 each at the end of first year, second year and third year from now. A client having a rate of interest at 10% p.a. can choose an option on the basis of the present values of both options as follows:
Option I:
The payment of Rs.2, 500 now is already in terms of the present value and therefore does not require any adjustment.
Option II:
The customer has to pay an annuity of Rs.900 for 3 years.

In order to find out the PV of a series of payments, the PVs of different amounts accruing at different times are to be calculated and then added. For the above example, the total PV is Rs.2, 238. In this case, the client should select option B, as he is paying a lower amount of Rs.2, 238 in real terms as against Rs.2, 500 payable in option A.
The present value of an annuity may be expressed as follows:

Illustration:
Find out the present value of a 5 years annuity of Rs.50, 000 discounted at 8%.
Solution:
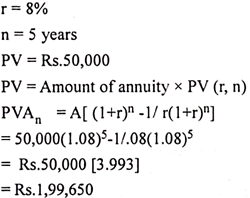
6. Techniques Used to Understand the Concept of Time Value of Money
Basically two techniques are used to find the time value of money.
They are:
1. Compounding Technique or Future Value Technique
2. Discounting Technique or Present Value technique
1. Compounding Technique:
Compounding technique is just reverse of the discounting technique, where the present sum of money is converted into future sum of money by multiplying the present value by the compound value factor for the required rate of interest and the period.
Hence Future Value or Compound Value is the ‘product’ of the present value of a given sum of money and the factor.
The simple formulas are used to calculate the Compound value of a single sum:
(a) If interest is compounded annually is-
FV = PV (1 + i)n = PV (CVFni)
Note- (1 + i)n is the formula for future value or compound value factor and
CVFni = Compound Value factor for the given number of years at required rate of interest.
(b) If Interest is added semi-annually and other compounding periods-

2. Discounting Technique or Present Value Technique:
Discounting technique or present value technique is the process of converting the future cash flows into present cash flows by using an interest rate/time preference rate/discount rate.
The simple formula used to calculate the Present Value of a single sum is:

Where;
P= Present Value, PVF= Present value factor of Re.1, DF= Discount factor of Re.1, A= Future Value or Compound Value, i = interest rate & n= number of years or time period given for 1 to n years and (1 + i)n = The compound value factor.
So from the above formula, it is very clear that the present value of future cash flows is the product of the ‘future sum of money and the discount factor’ or ‘the quotient of the future sum of money and the compound value factor (1 + i)1-n.
Note – Present value can be computed for all types of cash flows, say single sum/ multiple sums, even / annuity sums and mixed/un-even sums.
Alternatively, PVF/DF, CVF of a rupee and also the annuity discount factor (PADF) and the compound value annuity factor (CVAF) at the given rate of interest for the expected period can be referred through the tables also.
7. Present Value Technique or Discounting Technique
It is a process of computing the present value of cash flow (or a series of cash flows) that is to be received in the future. Since money in hand has the capacity to earn interest, a rupee is worth more today than it would be worth tomorrow.
Discounting is one of the core principles of finance and is the primary factor used in pricing a stream of future receipts. As a method, discounting is used to determine how much these future receipts are worth today.
It is just the opposite of compounding where compound interest rates are used in determining the present value corresponding to a future value. For example, Rs. 1,000 compounded at an annual interest rate of 10% becomes Rs. 1,771.56 in six years.
Conversely, the present value of Rs. 1,771.56 realized after six years of investment is Rs. 1,000 when discounted at an annual rate of 10%. This present value is computed by multiplying the future value by a discount rate. This discount rate is computed as reciprocal of compounding.
Present value calculations determine what the value of a cash flow received in the future would be worth today (that is at time zero). The process of finding a present value is called discounting; the discounted value of a rupee to be received in future gets smaller as it is applied to a distant future.
The interest rate used to discount cash flows is generally called the discount rate. How much would Rs.100 received five years from now be worth today if the current interest rate is 10%?
Let us draw a timeline.
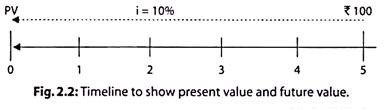
The arrow represents the flow of money and the numbers under the timeline represent the time period. It may be noted that time period zero is today, corresponding to which the value is called present value.
A generalized procedure for calculating the future value of a single amount compounded annually is as given below:

I. Ascertaining the Present Value (PV):
The discounting technique that facilitates the ascertainment of present value of a future cash flow may be applied in the following specific situations:
(a) Present Value of a Single Future Cash Flow:
The future value of a single cash flow may be ascertained by applying the usual compound interest formula as given below:

Let us understand the computation of present value with the help of an example that follows:
Example:
Mr. Aman shall receive Rs.25,000 after 4 years. What is the present value of this future receipt, if the rate of interest is 12% p.a.?

(b) Present Value of Series of Equal Cash Flows (Annuity):
An annuity is a series of equal cash flows that occur at regular intervals for a finite period of time. These are essentially a series of constant cash flows that are received at a specified frequency over the course of a fixed time period. The most common payment frequencies are yearly, semi-annually, quarterly and monthly.
There are two types of annuities – ordinary annuity and annuity due. Ordinary annuities are payments (or receipts) that are required at the end of each period. Issuers of coupon bonds, for example, usually pay interest at the end of every six months until the maturity date. Annuity due are payments (or receipts) that are required in the beginning of each period.
Payment of rent, lease etc., are examples of annuity due. Since the present and future value calculations for ordinary annuities and annuities due are slightly different, we will first discuss the present value calculation for ordinary annuities.
The formula for calculating the present value of a single future cash flow may be extended to compute present value of series of equal cash flow as given below:

Example:
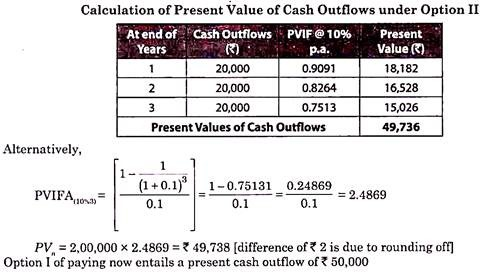
An LED TV can be purchased by paying Rs.50,000 now or Rs.20,000 each at the end of first, second and third year respectively. To pay cash now, the buyer would have to withdraw the money from an investment, earning interest at 10% p.a. compounded annually. Which option is better and by how much, in present value terms?
Solution:
Let paying Rs.50,000 now be Option I and payment in three equal installments of Rs.20,000 each be Option II, the present value of cash outflows of Option II is computed as:
(c) Present Value of a Series of Unequal Cash Flows:
The formula for computing present value of an annuity is based on the assumption that cash flows at each time period are equal.
However, quite often cash flows are unequal because profits of a firm, for instance, which culminate into cash flows, are not constant year after year.
The formula for calculating the present value of a single future cash flow may be extended to compute present value of series of unequal cash flows as given below:
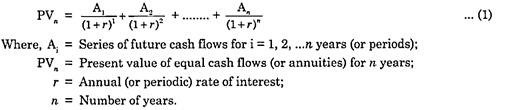
Example:
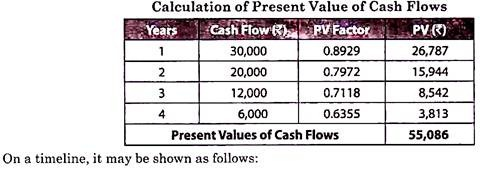
Ms. Ameeta shall receive Rs.30,000, Rs.20,000, Rs.12,000 and Rs.6,000 at the end of first, second, third and fourth year from an investment proposal. Calculate the present value of her future cash flows from this proposal, given that the rate of interest is 12% p.a.
Solution:

Implication:
If Ms. Ameeta lends Rs.55,086 @ 12%p.a, the borrower may settle the loan by paying Rs.30,000, Rs.20,000, Rs.12,000 and Rs.6,000 at the end of first, second, third and fourth year.
(d) Perpetuity:
It refers to a stream of equal cash flows that occur and last forever. This implies that the annuity that occurs for an infinite period of time turns it to perpetuity. Although it may seem a bit illogical, yet an infinite series of cash flows have a finite present value.
Examples of Perpetuity:
(i) Local governments set aside funds so that certain cultural activities are carried on a regular basis.
(ii) A fund is set-up to provide scholarship to meritorious needy students on a regular basis.
(iii) A charity club sets up a fund to provide a flow of regular payments forever to needy children.
The present value of perpetuity is computed as:

Example:
A philanthropist wishes to institute a scholarship of Rs.25,000 p.a., payable to a meritorious student in an educational institution. How this amount should he invest @ 8% p.a. so that the required amount of scholarship becomes available as yield of investment in perpetuity.

Valuation of Preference Shares:
Preference shares have preference over ordinary shares in terms of payment or dividend and repayment of capital if the company is wound up. They may be issued with or without a maturity period.
The preference shares unlike bonds has an investment value as it resembles both bond as well as common stock. It is a hybrid between the bond and the equity stock. It resembles a bond as it has a prior claim on the assets of the firm at the time of liquidations.
Like the common stock the preference shareholders receive dividend and have similar features as common stock and liabilities at the time of liquidation of a firm.
Types of Preference Shares:
a. Redeemable preference shares are shares with maturity.
b. Irredeemable preference shares are shares without any maturity.
Features of Preference Shares:
i. Dividend
The dividend rate is fixed in the case of preference shares.
ii. Claims
Preference shareholders have a claim on assets and income prior to ordinary shareholders.
iii. Redemptions
Redeemable preference shares have a maturity date while irredeemable preference shares are perpetual.
iv. Conversions
A company can issue convertible preference shares and can be converted as per the norms.
Valuation of Equity Shares
Equity Shares:
Equity shares are also referred to as common stock, unlike bonds, equity shares are instruments that do not assure a fixed return.
Equity is fundamentally different from debt. Debt is commonly issued by security known as bond/debenture. Financial markets deal with the transfer of these securities from one person to another. The price at which such transfer takes place is determined by market forces.
Features of equity share:
(a) Ownership and management,
(b) Entitlement to residual cash flows,
(c) Limited liability,
(d) Infinite life,
(e) Substantially different risk profile.
Challenges in Valuation of Equity:
The valuation of equity shares is relatively more difficult.
The difficulty arises because of two factors:
(i) Rate of Dividend on Equity Shares is not known.
(ii) Estimates of the Amount and timing of the cash flows expected by equity shareholders are more uncertain.
9. Risk and Return Analysis
What is risk?
Risk is the variability which may likely to accrue in future between the expected returns and the actual returns. So, the risk may also be considered as a chance of variation or chance of loss.
Types of Risk:
Risk can be classified in the following two parts:
1. Systematic Risk or Market Risk:
Systematic risk is that part of total risk which cannot be eliminated by diversification. Diversification means investing in different types of securities. No investor can avoid or eliminate this risk, whatsoever precautions or diversification may be resorted to. So, it is also called non diversifiable risk, or the market risk.
This part of the risk arises because every security has a built in tendency to move in line with the fluctuations in the market. The systematic risk arises due to general factors in the market such as money supply, inflation, economic recession, industrial policy, interest rate policy of the government, credit policy, tax policy etc. These are the factors which affect almost every firm.
2.Unsystematic Risk:
The unsystematic risk is one which can be eliminated by diversification. This risk represents the fluctuation in returns of a security due to factors specific to the particular firm only and not the market as a whole.
These factors may be such as worker’s unrest, strike, change in market demand, change in consumer preference etc. This risk is also called diversifiable risk and can be reduced by diversification. Diversification is the act of holding many securities in order to lessen the risk.
The effect of diversification on the risk of a portfolio is represented graphically in the below figure:
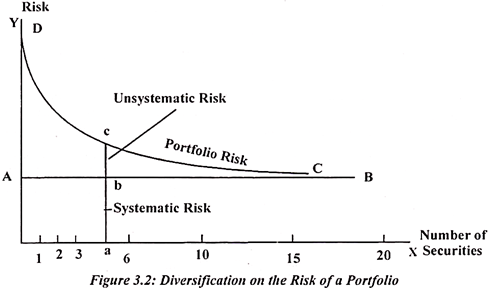
The above diagram shows that the systematic risk remains the same and is constant irrespective of the number of securities in the portfolio as shown by OA in the above diagram and is fixed for any number of securities.
For only security it is OA & for 20 security also it is OA. However, the unsystematic risk is reduced when more and more securities are added to the portfolio. As from the above diagram we can see that earlier it was OD & by increasing the number of securities it decreases to C.
10. Methods of Risk Management
Risk is inherent in business and hence there is no escape from the risk for a businessman. However, he may face this problem with greater confidence if he adopts a scientific approach by dealing with risk. Risk management may, therefore, be defined as adoption of a scientific approach to the problem dealing with risk faced by a business firm or an individual.
Broadly, there are five methods in general for risk management:
i) Avoidance of Risk
A business firm can avoid risk by not accepting any assignment or any transaction which involves any type of risk whatsoever. This will naturally mean a very low volume of business activities and losing of too many profitable activities.
ii) Prevention of Risk
In case of this method, the business avoids risk by taking appropriate steps for prevention of business risk or avoiding loss, such steps include adaptation of safety programmes, employment of night security guard, arranging for medical care, disposal of waste material etc.
iii) Retention of Risk
In the case of this method, the organization voluntarily accepts the risk since either the risk is insignificant or its acceptance will be cheaper as compared to avoiding it.
iv) Transfer of Risk
In case of this method, risk is transferred to some other person or organization. In other words, under this method, a person who is subject to risk may induce another person to assume the risk. Some of the techniques used for transfer of risk are hedging, sub-contracting, getting surety bonds, entering into indemnity contracts etc.
v) Insurance
This is done by creating a common fund out of the contribution (known as premium) from several persons who are equally exposed to the same loss. Fund so created is used for compensating the persons who might have suffered financial loss on account of the risks insured against.
11. Types of Investors
There are three types of investor which may be classified as:
a) Risk Averse
Under this category those investors appear who avoid taking risk and prefer only the investments which have zero or relatively lower risk. These investors ignore the return from the investment. Generally risk averse investors are – Retired persons, Old age persons and Pensioners.
b) Risk Seekers
Under this category those investors are nominated who are ready to take risk if the return is sufficient enough (according to their expectations). These investors may be ready to take – Income risk, Capital risk or both.
c) Neutrals
Under this category those investors lie who do not care much about the risk. Their investments decisions are based on consideration other than risk and return.
What is return?
Return is the amount received by the investor from their investment. Everyone needs high returns over invested amounts. Each and every investor who invests or wants to invest their amount in any type of project, first expects some return which encourages them to take risk.
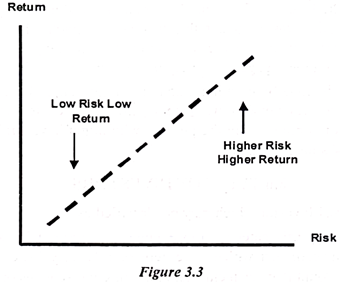
Risk and Return Trade Off:
The principle that potential “return rises with an increase in risk”. Low levels of uncertainty (low risk) are associated with low potential returns, whereas high levels of uncertainty (high risk) are associated with high potential returns. According to the risk-return tradeoff, invested money can render higher profits only if it is subject to the possibility of being lost.
Because of the risk- return tradeoff, you must be aware of your personal risk tolerance when choosing investments for your portfolio. Taking on some risk is the price of achieving returns; therefore, if you want to make money, you can’t cut out all risk. The goal instead is to find an appropriate balance – one that generates some profit, but still allows you to sleep at night.
We can see this in the following figure:
Risk and return analysis emphasizes over the following characteristics:
(i) Risk and Return have parallel relations.
(ii) Return is fully associated with risk.
(iii) Risk and return concepts are basic to the understanding of the valuation of assets or securities.
(iv) The expected rate of return is an average rate of return. This average may deviate from the possible outcomes (rates of return).