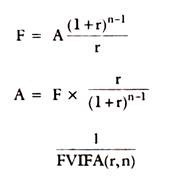In this article we will discuss about the concept and methods for time preference of money along with its applications.
Concept and Methods for Time Preference of Money:
We prefer today’s money to that of tomorrow due to our pressing needs for consumption and cost of abstinence from the present consumption, fall in the value of money of tomorrow due to inflation and possible use of money when exchanged for tomorrow’s money. Thus, when we lend money, we forego all the advantages of liquidity, ready usability, pressing needs, safety, etc. We abstain from present consumption when lent to somebody, or invested. All these will lead to what is called the time preference for money. To compensate for that, future money will have to be discounted to the present time, because both are not the same. Future money has to be more say 120, if the present money is Rs. 100, taking a discount factor of 20%, on one year.
Tomorrow’s money or money a year hence has to be discounted to the present day by discount rate suitable as a reward for the above sacrifices. This is called discounting, used for cash flows or dividends to be received in future and to be calculated for the present.
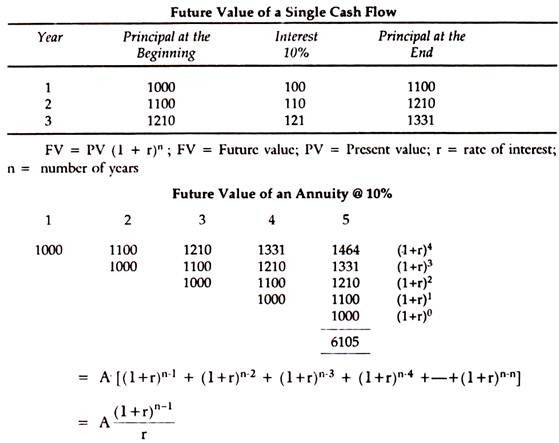
Similarly, an investment of today, if it is to be returned after a year or so, today’s money has to be compounded by a discount rate to equate to the future funds likely to be available in return. This is called compounding. Compounding and discounting are thus two major methods of analysing the time value of money.
ADVERTISEMENTS:
If we need to estimate the present value of future flows, then the Discounting Method is used. If we want the future value of present investment, we have the Compounding Method. Both help the decision-making process in investment in securities.
1. Discounting Method:
If the future value of the present investment is Rs. 116 at the end of 3 years and if it is discounted to the present day at 5%, then it will be equal to Rs. 100 at present.
The formula for PV (present value)-
Ct represents the cash flows, t for period of years and r is the discount rate or is called internal rate of return in the exercises of capital budgeting.
Take an example: r = 8%, payable once a year and t is 5 years and the factor value — summation of cash flows is Rs. 100.
This Formula also applies to one period return of Rs. 100 at the end of 5 years, the present value of which is Rs. 68 at a rate of return of 8%.
ADVERTISEMENTS:
2. Compounding Method:
If the interest rate is 5% and PV is Rs. 100, the future value one year hence will be Rs. 105, by using the formula of = 100 (1 + 0.5)1 = 105.
In two years, it becomes 100 (1 + 0.5)2 = 110.25
In three years it becomes 100 (1 + 0.5)3 = 115.76 and so on.
In the case of discounting, it is the reverse of the above formula, namely,
For the same three year period, at the end of 3 years, the future value should be Rs. 100 for investing Rs. 86.4 at present.
These formulae are based on some critical assumptions of constant flow of cash every period, the same reinvestment rate and the period is fixed.
Applications of Time Preference of Money:
In purchase or sale of a share, bond, or debenture, the price we pay has to be compared to the value of future flows in terms of dividends, or interest and future price realised. The principle of buy low and sell high has to be applied after an analysis of the present value of future flows of dividends, bonus, visible rights etc., as compared to the present price paid for it.
Sinking Fund Factor:
Present Value of an Annuity @ 10%:
ADVERTISEMENTS:
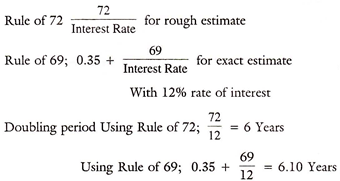
Doubling Period:
Shorter Compounding Period:
ADVERTISEMENTS:
If Interest is Credited Quarterly @ 12 % per annum
Effective rate of interest =12.551%
Where,
k = Nominal rate of interest
ADVERTISEMENTS:
m = Number of times compounding is done during a year
n = Number of years for which compounding is done.