AVM is based on a principle that the current value of money is worth more than the same amount of money in future.
In other words, the real worth or purchasing power of a specific amount of money changes with time. For example, the purchasing power of Rs. 100 would not be same after one year.
Therefore, money is preferred to be received in the present than any future date.
Similarly, if different projects yield the same return at different periods of time, the project with the earliest return would be preferred. The value of money decreases with time because the money available at present can be invested to earn returns from it. However, the money received in future loses the investment opportunity available at present. For example, if a project gives a return of Rs. 50,000 at present, the same amount can be invested in other profitable projects to earn more returns.
ADVERTISEMENTS:
On the other hand, if the same return is received from the project after two years, the investment opportunity of the amount for two years would be lost. Therefore, the project that gives a return of Rs. 50,000 at present should be selected. The present and future value of money can be calculated by using different formulae. Let us learn how to calculate the actual value of money in present and future.
Future Value of Cash Flows:
The future value refers to the real worth of any cash flow or a series of cash flows in future. Suppose a project generates a profit of Rs. 1000. If the amount of total generated profit is invested in another project that ensures 5% annual rate of return, the total amount received after one year would be Rs. 1050.
Therefore, it can be said that the future value of Rs. 1000 after one year would be Rs. 1050 at the rate of 5% per annum. Now, let us learn how to calculate the future value of a single cash flow and annuity (a set of fixed cash flows).
Future Value of a Single Cash Flow:
The future value of a single cash flow is the real value of a particular sum of money in future. For example, if a project needs an investment of Rs1,000 at present, and would yield return at the rate of 5% after one year starting from the current date. The return from the project after one year would be the future value of money invested in the project.
ADVERTISEMENTS:
Therefore, money received after one year = Principal + Interest
= 1000 + (1000 × 0.05)
= 1000 + 50 = Rs. 1050
Therefore, Rs. 1050 is the future value of Rs. 1000 after one year at the rate of 5% per annum. Similarly, Rs. 1050 is reinvested for another year; the amount received at the end of the second year would be Rs. 1102.5.
ADVERTISEMENTS:
Therefore, money received after two years = Principal + Interest
= 1050 + (1050x 0.05)
= 1050 + 52.50 = Rs. 1102.50
Therefore, the future value of Rs. 1000 after two years at 5% annual rate of return is Rs. 1102.5.
Now, the formula for calculating the future value of a single cash flow would be derived. Let us assume P is the principle amount, i represents the annual rate of interest, n is the number of years before the pay-off, and is the future value of the amount invested.
Future Sum = Principal + Interest
Therefore, the future value after one year F1 = P + P × i = P (1+i)
Similarly, the future value after second year F2 = F1 + F1 × i = F1 (1+i) = P (1+i) (1+i) = P (1+i) 2
Similarly, after three years, the future value would be equal to P (1+i) 3. Therefore, we can generalize the equation by saying that the future value of the amount P after nth year would be P (1+i) n
Future Value of Annuity:
ADVERTISEMENTS:
An annuity is a fixed and regular cash flow over a period of time. The future value of an annuity refers to the actual value of fixed and regular cash flows at a certain period of time in future. A project needs investments over a period of time. Therefore, the future value of the total investment made in a project can be determined by calculating the future value of annuity.
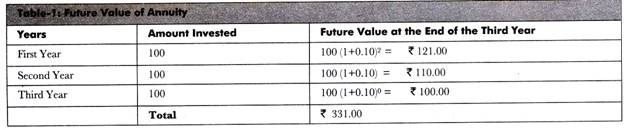
Imagine a scenario where Rs. 100 is invested at the end of every year for a period of three years at the rate of interest 10% per annum. What would be the future value of Rs. 100 after three years? The future value of money cannot be calculated by using the same formula for determining the future value of a single cash flow.
In this case, Rs. 100 invested at the end of first year would yield interest for two years, and Rs. 100 invested at the end of second year would generate interest for one year. Similarly, Rs. 100 invested at the end of third year would not yield any interest. Therefore, it becomes complex to calculate the total future value of cash.
Table-1 shows the calculation of future value of Rs 100:
ADVERTISEMENTS:
As shown in Table-1, the future value of a given annuity is Rs. 331 at the end of the third year.
If we generalize the preceding Table-1, we can say that F3 = A (1 +i) 2 +A (1 +i) 1 + A (1 +i) 0 = A [(1 +i) 2 + (1 +i) 1 + (1 +1) 0]
Where, A is the amount of annuity
ADVERTISEMENTS:
Similarly, for n number of intervals, the equation would be Fn = A [(1+i) n -1]/i [(1+i) n – 1]/i is called the Compound Value Factor of an Annuity (CVFA).
Present Value of Cash Flows:
The present value of cash flows is opposite to the future value of cash flows. Present value is the current value of the future cash flow over a fixed period of time at a specified rate of return. The present value of cash flow is always lesser than the future value of cash flow.
In brief, we can say that the amount of money received today would always be greater than received in the future. Suppose a project would give a return of Rs. 50000 after three years. Then, Rs. 50000 received after three years would not have the same value as of now. Therefore, one cannot decide the actual profitability of a project without determining the value of returns it generates at present.
On the other hand, a project may also yield returns at different periods of time. In such cases, the present value of the total return from the project can be determined by calculating the total present value of all the annual returns. Let us now learn how to calculate the present value of a single cash flow and annuity (a set of fixed cash flows).
Present Value of a Single Cash Flow:
The present value of a single cash flow is just opposite to the future value of a single cash flow. The present value of a single cash flow refers to the current value of money received in the future, whereas the future value of a single cash flow is the future value of money available at present.
In the above,we have calculated that Rs. 1050 is the future value of Rs. 1000 at the interest rate of 5 % per annum at the end of first year and Rs. 1152.5 at the end of the second year.
ADVERTISEMENTS:
Therefore, it can be said that the present value of Rs. 1050 received after one year and Rs. 1152.5 received after two years, is Rs. 1000. The formula for calculating the present value of a single cash flow can be derived from the formula of future value of a single cash flow, which is F1 = P + P × i = P (1+i).
Therefore, the formula for evaluating the present value of a single cash flow would be as follows:
Present Value (P) = F/ (1+i)
Similarly, the present value of a single cash flow after n number of years would be P = Fn [(1+i)-n]
Present Value of Annuity:
The present value of an annuity refers to the present value of all cash flows received in the future at equal intervals. The present value of an annuity cannot be determined by using the formula of calculating the present value of single cash flow.
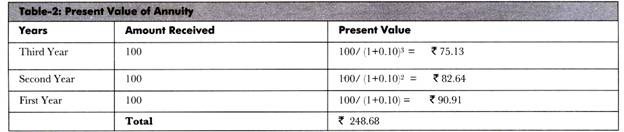
We can calculate the present value of an annuity by finding out the present value of the cash flow of each year and summing up those values. For example, a project is expected to provide a return of Rs. 100 at the end of each year for next three years at the interest rate of 10% per annum.
ADVERTISEMENTS:
The present value of Rs. 100 received after three years would be 100/ (1 + .10)3 = Rs. 75.13. Similarly, the present value of Rs. 100 received after two years is Rs. 82.64 and received after one year is Rs. 90.91. Therefore, the aggregate present value is 90.91+82.64+75.13= Rs. 248.68.
The calculation is shown in Table-2:
As depicted in Table-2, the present value of the given annuity is Rs. 248.63.
If we generalize the preceding Table-2, we can say that Present Value (P) = A/ (1+i) + A/ (1+i)2 +A/ (1+i)3 +…. +A/ (1+i)n
= A [1/ (1+i) + 1/ (1+i) 2 +1/ (1+i) 3 +1/ (1+i) n]