Hick’s Logical Theory of Demand: Preference Hypothesis and Logic of Ordering

In order to explain the behaviour of an ideal consumer Prof. Hicks assumes preference hypothesis as a principle which governs the behaviour of such a consumer.

The assumption of behavior according to a scale of preferences is known as preference hypothesis.

Hicks explains the meaning of preference hypothesis or behaviour according to the scale of preference as follows:

“The ideal consumer (who is not affected by anything else than current market conditions) chooses that alternative out of the various alternatives open to him, which he most prefers, or ranks most highly. In one set of market conditions he makes one choice, in others other choices; but the choices he makes always express the same ordering, and must, therefore, be consistent with one another. This is the hypothesis made about the behaviour of the ideal consumer.”

The above statement of Hicks implies that the consumer in a given market situation chooses the most preferred combination and he will choose different combinations in different market situations but his choices in different market situations will be consistent with each other.

It is important to remember that Hicks’ demand theory presented in Value and Capital’ was also based upon the preference hypothesis but there he expressed the given scale of preferences at once in the form of a set of indifference curves. This direct introduction of geometrical device has, as already noted above, various disadvantages and has, therefore, been given up. In ‘Revision of Demand Theory Hicks begins from the logic of ordering itself rather than starting from the geometrical application of it.

According to him, “the demand theory which is based upon the preference hypothesis turns out to be nothing else but an economic application of the logical theory of ordering.” Therefore, before deriving demand theory from preference hypothesis he explains the “logic of order”. In this context he draws out difference between strong ordering and weak ordering. He then proceeds to base his demand theory on weak-ordering form of preference hypothesis.

Strong and Weak Orderings Distinguished:

A set of items is strongly ordered, if each item has a place of its own in the order and each item could then be given a number and to each number there would be one item and only one item which would correspond. A set of items is weakly ordered if the items are clustered into groups but none of the items within a group can be put ahead of the others. “A weak ordering consists of a division into groups, in which sequence of groups is strongly ordered, but in which there is no ordering within the groups.”

It should be noted that indifference curves imply weak ordering in as much as all the points on a given indifference curve are equally desirable and hence occupy same place in the order. On the other hand, revealed preference approach implies strong ordering since it assumes that the choice of a combination reveals consumer’s preference for it over all other alternative combinations open to him. Choice can reveal preference for a combination only if all the alternative combinations are strongly ordered.

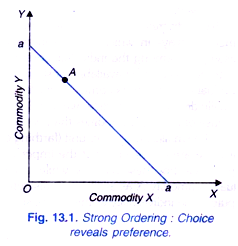
Weak ordering implies that the consumer chooses a position and rejects others open to him, then the rejected positions need not be inferior to the position actually chosen but may have been indifferent to it. Hence, under weak ordering, actual choice fails to reveal definite preference. The strong ordering and weak-ordering as applied to the theory of demand are illustrated in Fig. 13.1.

If the consumer is confronted with the price-income situation aa, then he can choose any combination that lies in or on triangle aOa. Suppose that our consumer chooses the combination A. Let us assume that our consumer is an ideal consumer who is acting according to his scale of preferences. Now, the question is how his act of choice of A from among the available alternatives within and on the triangle aOa is to be interpreted.

If the available alternatives are strongly ordered, then the choice of A by the consumer will show that he prefers A over all other available alternatives. In Samuelson’s language he ‘reveals his preference’ for A over all other possible alternatives which are rejected. Since, under strong ordering, the consumer shows definite preference for the selected alternative, there is no question of any indifferent positions to the selected one.

Hicks’ Criticism of the Logic of Strong Ordering:

Hicks criticises the logic of strong ordering. “If we interpret the preference hypothesis to mean strong ordering, we cannot assume that all the geometrical points, which lie within or on the triangle aOa represent effective alternatives. A two-dimensional continuum point cannot be strongly ordered.”

Prof. Hicks further says that if commodities are assumed to be available only in discrete units, so that the diagram is to be conceived as being drawn on squared paper and the only effective alternatives are the points at the corners of squares and therefore the selected point must also lie at the corner of a square, then the strong ordering hypothesis is acceptable.

Since in the real world, commodities are available in discrete units, therefore the strong ordering hypothesis should not present any difficulty. But Hicks contends that the actual commodities may be available in integral number of units but this cannot be said of the composite commodity money, which is usually measured on the V-axis.

Hicks regards money to be finally divisible. To quote him:

“If everyone of the actual commodities into which M can be exchanged is itself only available in discrete units; but if the number of such commodities is large, there will be a large number of ways in which a small increment of M can be consumed by rearrangement of consumption among the individual commodities, whence it will follow that the units in which M is to be taken to be available must be considered as exceedingly small.

And as soon as any individual commodity becomes available in units that are finally divisible, M must be regarded as finally divisible. In practice, we should usually think of M as being money, held back for the purchase of other commodities than X; though money is not finally divisible in a mathematical sense, the smallest monetary unit (farthing or cent) is so small in relation to the other units with which we are concerned that the imperfect divisibility of money is in practice a thing of no importance.

For these reasons, while it is a theoretical improvement to be able to regard the actual commodity X as available in discrete units it is no improvement at all to be obliged to impute same indivisibility to the composite commodity M. It is much better to regard money as finally divisible.

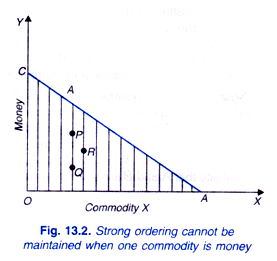
So, according to Hicks, where the choice is between any good which is available in discrete units and money which is finally divisible, the possibility of equally desired combinations must be accepted and strong ordering has, therefore, to be given up. Why the strong ordering hypothesis is not valid when the choice is between money which is finally divisible and is represented on the Y-axis and the commodity X which is imperfectly divisible and is represented on the X-axis is illustrated in Fig. 13.2.

This is because when money measured on Y-axis is taken to be finally divisible, the effective alternatives will no longer be represented by square corners, they will appear in the diagram as a series of parallel lines (or stripes) as shown in Fig. 13.2. All points on the stripes will be effective alternatives but such alternatives cannot be strongly ordered “unless the whole of one stripe was preferred to the whole of the next stripe, and so on; which means that the consumer would always prefer an additional unit of X whatever he had to pay for it.” But this is quite absurd.

Thus, the effective alternatives appearing on the stripes cannot be strongly ordered. Again, suppose there are two alternatives P and Q on a given stripe which are such that P is preferred to R on another stripe, while R is preferred to Q. Given that, we can always find a point between P and Q on a given stripe which is indifferent to R.

It is thus evident that when various alternatives appear as a series of stripes, there can be a relation of indifference between some of them. Thus strong ordering cannot be maintained when various alternative combinations consist of the composite commodity money which is finally divisible and actual commodity which is available only in discrete units. “As soon as we introduce the smallest degree of continuity (such as is introduced by the ‘striped’ hypothesis) strong ordering has to be given up.”

The Logic of Weak Ordering:

After rejecting the strong ordering hypothesis. Hicks proceeds to establish the case for the adoption of the weak ordering hypothesis. As noted above, the weak ordering hypothesis recognizes the relation of indifference, while the strong ordering hypothesis does not. In the words of Hicks, “If the consumer’s scale of preferences is weakly ordered, then his choice of a particular position A does not show (or reveal) that A is preferred to any rejected position within or on the triangle: all that is shown is that there is no rejected position which is preferred to A. It is perfectly possible that some rejected position may be indifferent to A; the choice of A instead of that rejected position is then a matter of ‘chance’.

From the above statement of Hicks it is clear that, under the weak ordering hypothesis, the choice of a particular combination does not indicate preference for that particular combination over another possible alternative combination but it only shows that all other possible alternative combinations within or on the choice triangle cannot be preferred to the chosen combination.

There is possibility of some rejected combinations being indifferent to the selected one. If preference hypothesis in its weak ordering form is adopted, then it yields so little information about the consumer’s behavior that the basic propositions of demand theory- cannot be derived from it.

Therefore, Hicks has felt it necessary to introduce an additional hypothesis along with the adoption of the weak ordering hypothesis so as to derive basic propositions of demand theory. This additional hypothesis which is introduced is simply that ‘the consumer will always prefer a larger amount of money to a smaller amount of money, provided that the amount of good X at his disposal is unchanged.

It should be carefully noted that it is not necessary to make this additional hypothesis if strong ordering form of preference hypothesis is adopted. But this additional hypothesis which has been introduced by Hicks is very reasonable and is always implicit in economic analysis, even though it is not explicitly stated every time.

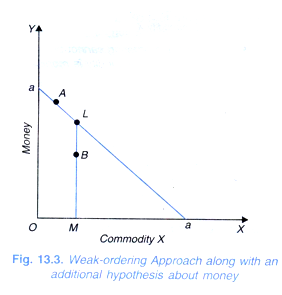
Now the question is what positive information is provided by weak ordering approach when supported by the above additional hypothesis. Let us consider Fig. 13.3. From all the available combinations within and on the triangle aOa the consumer chooses A. Under weak ordering hypothesis alone the choice of A rather than B which lies within the triangle aOa does not show that A is preferred to B; it only shows that B is not preferred to A. In other words, under weak ordering alone, the choice of A rather than B means that either A is preferred to B, or the consumer is indifferent between A and B.

Now, consider the position L which lies where the stripe through B meets the line aa. On the additional hypothesis made, L is preferred to B, since L contains more amount of money than B, amount of X being the same in both the positions. If A and Bare indifferent, then from the transitivity it follows that L is preferred to A. But L was available when A was selected. Therefore, though L can be indifferent to A, it cannot be preferred to A.

Thus, it follows that the possibility that A and B are indifferent must be ruled out. Hence, when we adopt the weak ordering along with the additional hypothesis we come to the conclusion that the chosen combination A is preferred to any combination such as B which lies within the triangle. What cannot be said with certainty under weak ordering even with the additional hypothesis is whether the chosen combination A is preferred to a combination such as L which lies on the triangle, that is, on the line aa. A can be either preferred to L or indifferent to it.

Drawing the difference between the implications of strong and weak orderings. Hicks says. “The difference between the consequences of strong and weak ordering so interpreted amounts to no more than this: that under strong ordering the chosen position is shown to be preferred to all other positions within and on the triangle, while under weak ordering it is preferred to all positions within the triangle, but may be indifferent to other positions on the same boundary as itself.”

It will be evident from above that the difference between the effects of the strong and weak orderings is very small and that it only affects a class of limiting cases (i.e., positions lying on the triangle). The weak ordering theory, Hicks says, “has a larger tolerance and, therefore, it deals with these limiting cases rather better”. Apart from this, weak ordering hypothesis, contends Hicks, is more useful and desirable.

“If we take the strong ordering approach, we are committing ourselves to discontinuity not merely to the indivisibility of the particular commodity, demand for which is being studied, but also to the indivisibility of the composite commodity used as a background. If, on the other hand, we take the weak ordering approach, we are committing ourselves to some degree of continuity but divisibility of the background commodity is itself quite sufficient to ensure that the weak ordering approach is practicable.”

As stated above, the weak ordering approach to be useful for demand theory requires an additional assumption to be made, namely, that the consumer prefers a larger amount of money to a smaller amount. Further, another assumption which is to be necessarily made when the weak ordering approach is adopted is that the preference order is transitive. These two additional assumptions are not required in the case of strong ordering approach.