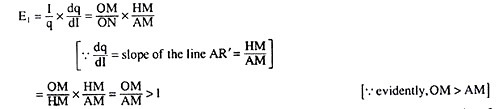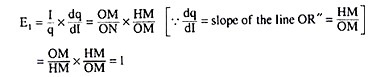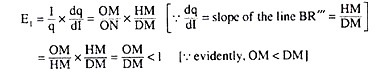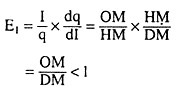Engel Curve and Income-Elasticity of Demand (With Diagram)

In this article we will discuss about the Engel curve and income elasticity of demand, explained with the help of diagrams.

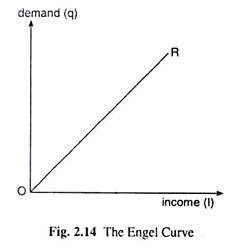
The Engel Curve for a good is a relation of functional dependence between the income of the buyers and the demand for the good. The Engel Curve gives us the quantity demanded of the good at any particular income level of the buyers, all other demand determinants remaining unchanged.

Therefore, from the Engel curve it can be known how would demand for the good would change when there is a change in the buyers’ income.

That is why the income-elasticity of demand is defined at any (income, demand) point on the Engel Curve. In our example (given above), the index for money income of 150 and the quantity demanded of 300 units is a particular point (150, 300) on the Engel Curve. At this point, E_I = 2 is obtained.

The curve in Fig. 2.14 is the Engel Curve for a good. This Engel Curve is obtained from the Engel Curves of indi­vidual buyers for the good. Here it has been assumed that the demand for the good changes in the same direction as the income of the buyers. That is why the curve has been obtained to be positively sloped. In such a case, the value of E_I would also be positive, E_I = 2 is obtained.

Now, if the demand for a good (measured along the vertical axis) decreases or remains unchanged as the income of the buyers (measured along the horizontal axis) increases, i.e., if the slope of the Engel Curve for the good be negative or zero, then the (propor­tionate or p.c.) change in demand would be negative or zero, respectively, and, consequently, the value of E_I would also be negative or zero.

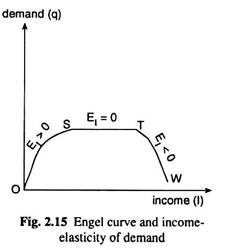
In Fig. 2.15, a Engel Curve is drawn for a good, OSTW. Since the slope of the OS segment of this curve is positive, the income-demand relation here would be posi­tive and E_I also would be positive (E_I > 0). Again, the seg­ment ST of this curve is a horizontal straight line, and so, here, the slope of the curve is zero, and E_I also would be zero (E_I = 0).

Over this segment, demand for the good is independent of income. Lastly, the segment TW of the Engel curve is negatively sloped, and so the income-demand relation here is negative and E_I also would be negative (E_I < 0).

Income-Elasticity of Demand and Slope of the Engel Curve:

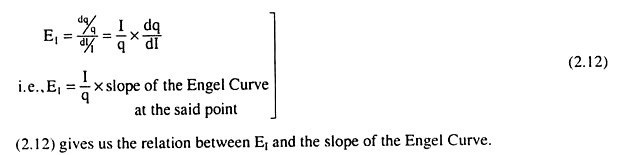
At any (I, q) point on the Engel Curve for a good, it is obtained:

 

 

 

 

 

 

Straight Line Engel Curve and E_I:

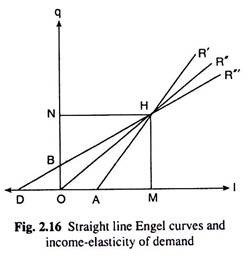
If the Engel Curve is a positively sloped straight line then, at any point on this curve, E_I > 1, if the line starts from a point on the positive side of the horizontal axis, E_I = I, if the line starts from the point of origin and, E_I < 1, if the line starts from a point on the positive side of the vertical axis. These points can be established with the help of Fig. 2.16.

In this figure, the straight line Engel curve AR’ has met the horizontal axis at the point A on its positive side.

At any point H (I, q) on this line, It is obtained:

Now, in the second case, the straight line Engel Curve OR’’ has started from the point of origin.

At any point H (I, q) on this line, It is obtained:

Lastly, the straight line Engel Curve BR’’’ has started from the point B on the positive side of the axis.

At any point H (I, q) on this line, It is obtained:

It may be noted here that the point H on the three Engel lines in Fig. 2.16 are any three points on these lines. They are not necessarily the same point as taken for the sake of neatness of the diagram. In other words, the point H is not necessarily the point of intersection of any two or of all the three of the Engel lines that are given in Fig. 2.16.

Curvilinear Engel Curve and E_I:

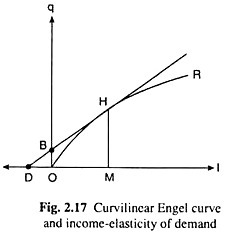
If the Engel Curve for any good be curvilinear, then the slope of the curve at any point would be equal to the slope of the tangent to the curve at the said point.

That is why, if this tangent meets the horizontal or the vertical axis at some point on the posi­tive side (of the axis), respectively, E_I > 1 or E_I < 1, and if the tangent meets the point of origin, E_I = 1. In Fig. 2.17, the curvilinear Engel Curve is OR, and the tangent at any point H (I, q) on this curve has met the vertical axis at the point B on the positive side. Now, at the point H, it is obtained

It may be shown in a similar way that if the tangent at any point on a curvilinear Engel Curve meets the horizontal axis at any point on its positive side, or if it meets the point of origin, then E_I > 1 or E_I = 1 can be obtained, respectively.