Input Demand for a Monopolist (With Diagram)

In this article we will discuss about the Input Demand for a Monopolist.

Thus far we have analysed profit maximization for a monopoly firm in terms of the output decision. As was the case for perfectly competitive firms, we may also analyse profit maximization in terms of input usage. To start with we consider the monopoly firm’s input decision assuming that it faces given (constant) prices for the inputs it purchases.

Input Prices Given:

Suppose a monopoly firm hires a single variable factor and faces a market-determined price for that factor. As in the case of competition when a monopolist employs an additional unit of the factor, output increases by an amount equal to the marginal physical product of the factor.

However, since price does not equal marginal revenue, for a monopoly to sell the large output, commodity price has to be reduced. Hence, total revenue does not increase by price times the marginal product of the factor input. Rather total revenue changes by marginal revenue times marginal product. This is the marginal revenue product of the input.

In the case of a competitive firm, VMP declines because marginal physical product falls (due to the operation of the laws of variable proportions). For a monopolist MRP declines, with increase in the usage of the input not only because marginal product declines, but also because MR declines as output is increased.

For example, suppose increasing the usage of the variable input by one unit increases output from 30 to 38 units; thus MPP = 8. Also suppose that the firm could sell 30 units at a price of Rs. 25 each; but to sell 38 units, price has to be reduced to Rs. 22.

Thus, the gross addition to total revenue from hiring the additional unit of the input is 8 (the added production) times Rs. 22 (the new selling price) or Rs. 8 x Rs. 22 = Rs. 176.

But to sell the additional 8 units, the price of the 30 units that could have been sold at Rs. 25, must fall by Rs. 3. Thus the lost revenue from the price reduction is Rs. 3 x 30 = Rs. 90. This loss must be subtracted from the gross gain to give a net gain of Rs. 176 – Rs. 90 = Rs. 86. This net gain — Rs. 86 — is the marginal revenue product of the input.

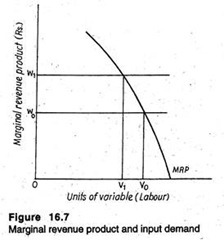
A monopolist’s demand for a single variable input is the positive portion of the MRP curve. Since both MP and MR decline, the input demand function must be downward sloping (from left to right).

In Figure 16.7, the relevant portion of MRP is shown. We start with the price of the input at w₀. The firm will hire V₀ units of the inputs at this price. It is quite obvious that the firm would not hire fewer than v₀, because an additional unit of input would add more to the firm’s revenue (MRP) than it costs (w₀).

It is quite clear that it would not hire more than V₀, because an additional unit of the input would add less than it costs the firm to hire that unit.

If the price of the input rises to w₁ the firm – decreases its usage of the input v₁ to amount at which MRP and w₁ are equated with, each other. Thus, it is observed that within the relevant range the MRP curve is the monopolist’s demand curve for a single factor of production.

The derivation of input demand curves is more complicated in the case of several variable inputs.

The MRP curve is no longer the demand for the input, because all the inputs are interdependent in the production process.

A change in the price of any one input leads to change not only in the usage of that input but in the use of other inputs, too. It may be recalled that the marginal product curve for an input was derived assuming the usage of all other inputs was held constant. Thus, changes in the rates of usage of other inputs shift the MRP curve.

However, the monopolist’s demand for an input continues to slope downward. And, what is more important is that the monopolist still uses that amount of each variable input at which its marginal revenue product equals its price.

For instance, if the monopoly firm uses three variable inputs — v₁,v₂ and v₃ — all of which have given market-determined prices — r₁r₂ and r₃ — the firm will maximize profit (or minimize loss) by employing each input such that the following conditions hold:

MRP_V1 = r₁

MRP_V2 = r₂

MRP_V3 = r₃

Since the inputs are interdependent in the production process, these conditions must hold at the same time. The implication is that the optimal levels of usage of the inputs have to be determined simultaneously.

Thus, if an input’s price is given to the monopoly we have the following principle.

Principle:

A monopolist’s demand for a variable factor has to be negatively sloped. Although the input demand curve, when more than one input is variable, is not the MRP curve, at every point on the demand curve, the price of the input equals its marginal revenue product.

Upward-Sloping Input Supply:

So long we have assumed that the price of an input is determined by supply and demand in the input market and is independent of the level of usage of the input by an individual firm. But monopoly firm is so large a part of the market as to have an appreciable effect upon the price of some of the inputs it uses.

In such situations, the firm has to pay a higher price if- it wishes to hire more units of the input. It not only has to pay more to the additional units of the resource hired but also must pay the higher price for all units, i.e., new as well as old units which could be hired at lower price.

Thus, the addition to cost is the cost of the added units hired plus the cost of paying more to the other units already being used. This extra cost is called the marginal factor cost of an input. Marginal factor cost exceeds the price of the input.

Therefore, if a monopoly faces an upward-sloping factor supply function, it will reach the point of optimum purchase of an input by equating the marginal revenue product of the input with the marginal factor cost of the input (rather than the input price):

MRP = MFC

In such a situation, the input price will be less than MFC.