The below mentioned article provides short notes on Choice of Revealed Preference.
Prof. Samuelson’s theory of demand is based on the revealed preference axiom or hypothesis which states that choice reveals preference. Keeping this fact into view, a consumer buys a combination of two goods either because he likes this combination in relation to others or this is cheaper than others.
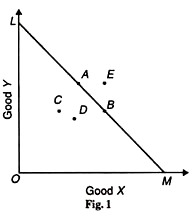
Suppose the consumer buys combination A rather than combination В, С or D. It means that he reveals his preference for combination A. He can do this for two reasons.
First, combination A may be cheaper than the other combinations В, C, D.
ADVERTISEMENTS:
Second, combination A may be dearer than others and even then he likes it more than other combinations. In such a situation, it can be said that A is revealed preferred to В, C, D or В, C, D are revealed inferior to A. This is explained in Figure 1.
Given the income and prices of the two goods X and Y. LM is the price-income line of the consumer. The triangle OLM is the area of choice for the consumer which shows the various combinations of X and Y on the given price-income situation LM.
In other words, the consumer can choose any combination between A and В on the line LM or between С and D below this line. If he chooses A, it is revealed preferred to B. Combinations С and D are revealed inferior to A because they are below the price-income line LM.
ADVERTISEMENTS:
But combination E is beyond the reach of the consumer being dearer for him because it lies above his price-income line LM. Therefore, A is revealed preferred to other combinations.
According to Prof. Hicks, when a consumer reveals his preference for a definite combination on the basis of observed market behaviour, he does so under strong ordering when the chosen position is shown to be preferred to all other positions within or on the triangle OLM.
So when the consumer reveals his definite preference for combination A within and on the OLM triangle, he rejects all other combinations such as В, С and D. Thus the choice of A is strongly ordered.