Equilibrium Level of National Income

What are the conditions for the attainment of equilibrium level of national income? Does ‘equilibrium income’ always indicate full employment?

Or, Discuss the theory of determination of the equilibrium level of national income on the basis of income-expenditure approach.

Or, Explain how equilibrium level of national income is deter­mined by aggregate expenditure in an economy.

National income, (GNI) or national output (GNP) is the total output available to satisfy peoples wants. A rising GNP implies economic growth. However, GNP does not always show a steady upward movement. Sometimes it moves up and sometimes it moves down. Thus economists are interested in knowing why GNP shows fluctuations. To answer this ques­tion we need a theory of national income determination.

Such a theory was first presented in a systematic way by J.M. Keynes in 1936. The theory which explains the level of national income and changes therein is called the theory of income determination. To be more specific, the theory of income determination seeks to find out the equilibrium level (value) of national income.

Assumptions:

The Keynesian theory of income determination is based on two assumptions:

(a) Wages and price are rigid. Thus, if aggregate demand increases production (GNP) will increase, wages and prices re­maining unchanged. In fact, Keynes assumed output adjustment and not price adjustment,

(b) The economy is having unemployed resource and idle capacity. This means that if aggregate demand increases it is possible to increase production immediately to meet the extra demand. Thus according to Keynes there is not such thing as ‘automatic full employment’ as has been postulated by the classical economists,

(c) Thirdly, all investment is autonomous and thus independent of national income (i.e., independent of income),

(d) Finally, consumption is partly autonomous and partly induced (i.e., dependent on income).

Two conditions:

According to Keynes two conditions have to be satisfied for attaining the equilibrium level of national income.

However, they are equivalent and are stated below:

Condition 1:

Desired expenditure equals income received. In a simple two-sector econ­omy business firms will produce anything they can sell at existing prices. So, total output (GNP), Y, will be equal to total desired expenditure which is the sum total of private consumption and private investment. Thus business firms will be eager to produce and sell whatever consumption goods, and investment goods people and business firms wish to buy.

This condition is stated as:

Y = E = C + I ………. (1)

where E is aggregate desired expenditure and is the sum total of consump­tion (C) and investment (I).

The above condition simply states that actual output, Y, will be equal, in equilibrium, to desired expenditure, E. If actual output is less than what consumers and business firms want to buy, output will increase. Firms will be eager to produce more output to meet the excess demand.

If actual output exceeds the demand for both consumption and capital (investment) goods, firms will be forced to cut-back production or reduce their output levels to avoid an endless (and undesired) accumulation of unsold stocks.

Condition 2:

The second condition is stated in terms of desired saving and desired investment. This condition implies that national income is in equilibrium when desired saving is equal to desired investment. This condition may now be explained. It is well known that disposable income is partly spent on consumption goods and partly saved; so whatever is not spent is automatically saved.

Thus we can write:

Y = C + S ……. (2)

It is also known that in our simple two-sector closed economy (without government centre) all expenditure is either for consumption or investment: E = C + I. Now, if we substitute this equation as also (2) into the equilibrium condition (1) we get

C + S = C + I ……. (3)

where C on the left hand side shows supply or output of consumption goods C on the right hand side shows demand for such goods. Now, if the commodity market is to be in equilibrium, the two must be equal. Hence they cancel out. Or, we get

S = I ……….. (4)

where S is the supply of capital goods (or savings) and 1 is the demand for capital goods (or investment).

Thus, S = I is a statement of the equilibrium condition given in equation (1). Saving is a leakage or withdrawal from the circular flow of income. Hence it acts as a contractionary force on the circular flow of income. In contrast, investment is an injection into the circular flow. Hence, it exerts an expansion­ary pressure on the circular flow of income.

Thus, national income is in equilibrium (i.e., national income remains unchanged and without a rise or a fall) when the contractionary pressure of saving is exactly balanced by the expansionary pressure of investment.

In the language of R. G. Lipsey, “Equilibrium income occurs when demanders are just willing to purchase everything produced or, equivalently, when the contractionary force exerted by saving just equals the expansionary force exerted by investment.”

A more detailed discussion of the equilibrium conditions (optional):

In a simple two-sector economy

E = C + I…….. (5)

This is a definitional equation

Here, I = I……….. (6)

This means that a fixed level of investment takes place at all levels of income. This is so because all investment is autonomous and thus independent of income. Investment depends on the marginal efficiency of capital and the rate of interest.

Consumption depends on income and the consumption equation is written as:

C = bY……….. (7)

where C is total consumption, b is MPC and Y disposable income. If b= 4/5, 80% of Y will be spent on consumption goods. Thus total consumption is MPC times disposable income (if we ignore autonomous consumption which is a very small component of total consumption).

Now, if we substitute (3) and (2) in equilibrium condition (1), i.e., Y=C + I, we get:

E = Y = C + I

or, Y = bY + l

or, Y = 1/1 – b I = I/1 – b = I/s

where s = 1 – b = MPS. Thus the simplest way to find out the equilibrium value of national income in Keynes’ two-sector demand-determined model is to divide the fixed level of autonomous investment by the MPS which is 1- MPC.

Now, if we use the second approach, i.e., the saving-investment approach we get the same condition: S = I, where S = s Y, i.e., total saving is MPS times disposable income.

Thus if we substitute the second equation in the first one we get:

sY = I where I = I

or, sY = I

or Y = I/s = I/MPS

Thus the two conditions are equivalent and give us the same result.

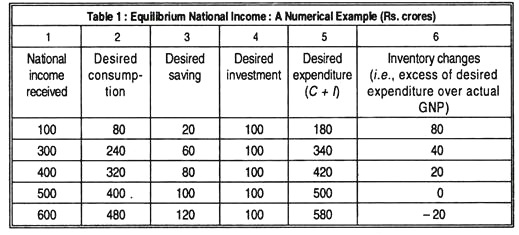
They may now be restated in two other ways: (a) numerically; and (b) graphically. We start with a numerical example. See Table 1.

 

A. The income-expenditure Approach:

Here, we assume that MPC is constant at 4/5 and MPS = 1/5, i.e., 80% of disposable income is spent on consumption goods and 20% is saved. Thus when income is 100 consumption is 80 and saving is 20. We also assume that a fixed investment of 100 takes place at all levels of income.

National income attains its equilibrium value when desired expenditure, C + I (= 500), equals actual output or GNP (500) and desired saving (100) equals desired investment (100). This may also be found out by dividing the fixed level of investment of 100 by the MPS. Since MPS = 1/5

Y = I/MPS = 100/V₅ = 500 MPS

If desired expenditure exceeds actual output firms will be eager to produce more to meet the extra demand. As a result output and income will rise. In contrast, if output produced exceeds desired expenditure, business firms will be forced to hold inventories of finished goods.

Since they cannot sell all they want, they will be induced to reduce production. As a result employment and national income will fall. The process will continue until un-designed, i.e., stocks of unsold goods get exhausted completely.

Table 1 makes it clear that if GNP were to be held at any level below Rs. 500 crores, consumers and business firms would be eager to buy more than was being produced. Desired expenditure, C + I would then exceed actual output. This cannot be an equilibrium position. For example, if output were Rs. 300 crores, desired expenditure would be Rs. 340 crores.

Since, in Keynes’ model, firms are assumed to produce sufficient output to meet current demand, they will be inclined to produce more. Consequently output will increase first to Rs. 400 crores and then again to Rs. 500 crores.

The converse is also true. If actual output exceeds Rs. 500 crores, desired expenditure is Rs. 580 crores. Thus, inventories (unsold stocks) of Rs. 20 crores would accumulate in each period. To prevent further accumulation of such stocks business firms would continue to reduce their output until they succeed in selling all they manage to produce.

It thus logically follows that the only possible equilibrium in Table 1 is at a GNP level of Rs. 500 crores. Desired expenditure is then just enough to buy what is produced, neither more nor less. At this level of GNP households spend Rs. 400 crores on consumption goods and save Rs. 100 crores.

But business firms make an investment (expenditure on capital goods) of Rs. 100 crores. Thus total desired expenditure is Rs. 500 crores, which is just enough to buy the current output (GNP) of Rs. 500 crores.

The logic of equilibrium:

What makes this particular level of output equilibrium? Equilibrium occurs at an output level of Rs. 500 crores because no other level can be sustained. These unintended inventory changes bring output into equality with total expenditure.

Table 1 shows the role of unintended inventory changes. If planned spend­ing or output exceeds current production, inventories decline. And business firms start realising that their production is not keeping pace with sales. Firms respond to these unintended inventory changes by increasing their levels of output.

In contrast, if current output exceeds planned spending, there would be an unintended inventory build up. Business firms would respond quickly to this by reducing output. These unintended inventory changes would prompt business firms to adjust their levels of production and move the economy to the unique level of national income and output at which Y = C + I. Thus inventory changes play a crucial role in this process.

B. The saving-investment Approach:

So long we have looked at the equilibrium in terms of the equality between desired expenditure and actual output (i.e., Y = C + I). The same equilibrium condition can be developed in terms of equality between desired saving and desired investment (S = I).

At the equilibrium level of national income or GNP, desired saving of Rs. 100 crores just equals desired investment of the same amount. In Keynes’ model, I = Rs. 100, i.e., since all investment is autonomous, it remains unchanged at all levels of income.

If GNP or national income is less than its equilibrium level, desired investment exceeds desired saving. The excess of injection over leakage exerts an expansionary pressure on national income. In contrast, above the equilibrium level of income, desired saving exceeds desired investment.

In this case the excess of desired leakage over desired injection exerts a contractionary pressure on national income. So, it logically follows that when desired S = desired I, the addition to aggregate demand caused by investment injection just equals the subtraction from aggregate demand caused by saving leakage (i.e., by households not spending all of their income).

At this stage desired expenditure (C + I) is just equal to actual output (GNP), indicating that all output that is produced will be bought by households and firms (in the form of consumption and capital goods, respectively), but no further demand will be created on society’s output.

A Graphical Interpretation:

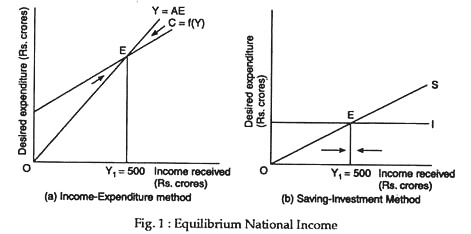
The data presented in Table 1 may now be represented graphically. This is done in Fig. 1. It has two parts. The first part illustrates the income-expenditure approach and the second part the saving-investment approach.

In part (b) we first draw a 45° -line called income line or guideline. Its slope is always one because it is the locus of all the points which have equal value on both axes, i.e., at any point on the line expenditure equals income.

Any point on the line could be interpreted as a possible equilibrium point because anywhere on it buyers are just ready to buy (E = C + I) exactly what is being produced (Y = GNP). Above the 45° line, desired expenditure (C + I) is exactly equal to output produced (income received); below the 45°-line, desired expenditure is less than national income.

A. The income-expenditure approach:

Part (a) of Fig. 1 illustrates how the equilibrium level of national income is arrived at by using the income-expenditure approach. It shows that the equilibrium level of national income occurs where the aggregate expendi­ture function intersects the 45° line.

Thus, E is the equilibrium point because at this point aggregate desired expenditure is exactly equal to national output. If income is less than Rs. 500 crores, desired expenditure exceeds output and output has to increase to meet the demand.

This point is indicated by the leftward pointing arrow. In contrast, at any income above Rs. 500 crores, desired expenditure will be less than output and output has to fall as is indicated by the right-upward pointing arrow.

B. The saving-investment approach:

Part (b) of Fig. 1 illustrates the saving-investment approach. It shows that the equilibrium value of national income is attained where the saving line (curve) intersects the investment line. Thus at point E₀, and only at this point, desired saving is equal to demand investment and the equilibrium level of national income occurs.

At any lower level of income, desired investment exceeds desired saving and national income will rise because injection to circular flow exceed leakage from it. At any income above the equilibrium, desired saving exceeds desired investment and national in­come falls for an exactly opposite reason.

Equilibrium without Full Employment:

In Keynes model we assume that the economy’s price level is fixed. Therefore any change in total spending or total income is entirely due to a change in the number of actual physical units of output produced by the economy. And this requires a change in the amount of labour used in production. Consequently each and every level of national income on the horizontal axis of Fig.1 corre­sponds to a different level of total income.

A major implication of the income-expenditure approach is that the level of employment associated with the equilibrium level of total income need not correspond to full employment, and typically will not.

For example, suppose that the labour force will be fully employed only when the economy produces the level of total output associated with a total income level equal to Rs. 800 crores. However, if the economy’s total expenditure schedule is E (Fig. 1) total spending (of Rs. 500 crores) is not sufficient to sustain this level of national income.

Consequently, some of the labour force will be unemployed. In general, the lower is the equilibrium level of national income, the higher is the unemployment rate. According to Keynes there are two obstacles to full employment, viz., (a) rigidity of wages and prices and (b) deficiency of demand (or purchasing power).

Thus, while classical unemployment is real-wage unemployment (un­employment due to excessive real usage) is demand-deficient unemploy­ment which is a typical problem of an economy in depression.