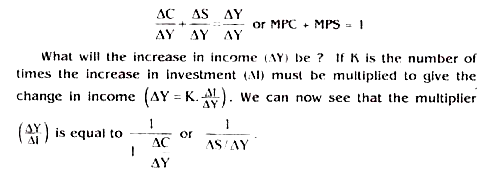Determination of National Income in a Close Economy!
In a closed economy, without trade, the national income can be described in a number of ways.
The national product and the national income are two sides of the same coin, and the national product equals, by definition, the national income.
Income produced is equal to income paid out, which is equal to income available for expenditure or. In other words, the value of consumption goods and services and investment goods produced is equal to the amount spent on consumption and the amount which goes into savings.
ADVERTISEMENTS:
C + I = Y = C + S …(1)
Where, C stands for goods consumed or produced, I investments, S savings and Y national income.
From this we then deduce that in equilibrium savings must equal investment, so that we get:
I = S …(2)
ADVERTISEMENTS:
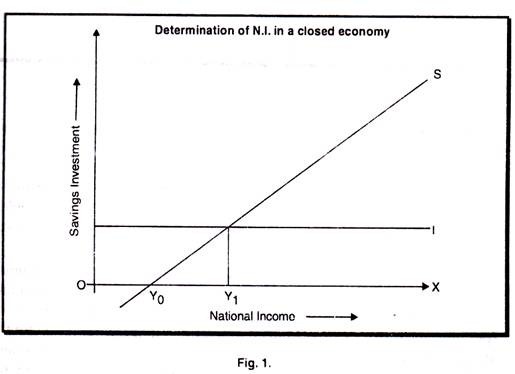
The economic meaning of this is that if producers plan to invest the same amount as the consumers plan to save, the national income is in an equilibrium position. The meaning of equilibrium here is that there are no forces which tend to move the national income from its given equilibrium. A geometric illustration of this simple idea is given in Fig.-1. Consumers can spend their income in two ways: they can consume it or save it. In Fig – 1, we take only savings – explicitly into account. From this we see that savings are a function of income; in mathematical terms,
S= S(Y) …(3)
At a certain low national income, nothing is saved; all income is
consumed. Savings are zero at the point where the savings schedule, s. In Fig. – 1 cuts the horizontal axis, denoting national income. This happens at Y0. If the national income falls below this point, savings are negative.
This implies that the country is consuming part of its stock of capital. Only at a national income larger than Yo will positive savings occur. The larger the national income, the more the country saves. Thus, savings are an increasing function of national income. The savings schedule, shown here as a straight line, indicates that marginally a constant fraction of national income is saved.
ADVERTISEMENTS:
Let us, for the sake of reasoning start by assuming that investment is independent of the level of national income. So that producers invest a constant amount, regardless of how small or how large the national income is, or in mathematical terms.
Io= Constant …(4)
Equilibrium in the national income is reached at the point where the savings schedule, denoting planned savings, cuts the investment schedule, denoting planned investment. This happens at Y1 the national income equilibrium.
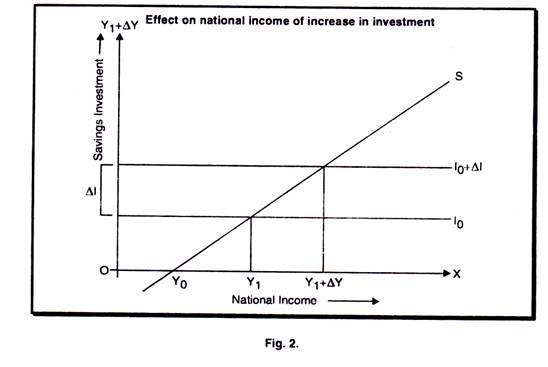
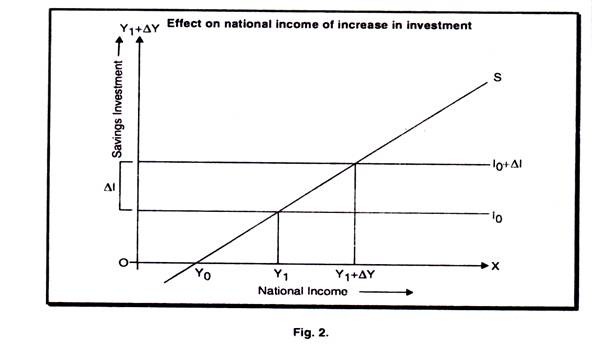
To understand the notion of equilibrium in national income and to discover what determines the level of national income let us assume that the behaviors of the producers or consumers changes. Let us start by assuming that producers plan to invest more. Such a changed in investment plan illustrated in Fig. 2. When producers decide to invest more, we get an upward shift in the investment schedule. The increase in investment we can denote ∆I, and the new investment schedule is therefore Io + ∆I. This causes the national income to expand, increasing by ∆Y from Y1 to Y2 + ∆Y.
When investment increases from Io to Io + ∆I then income changes from Y1 to ∆Y by a multiple factor K. The new investment will produce an initial increase in national income, which induces a further rise in spending (this time for consumption). As this, in turn, is spent, it increases income still further. The change in income from the original increase in investment includes the effect of all these subsequent responding.
If there were no savings, the original increase in investment would lead to an increase in income without limit, or to infinity. Actually, however, not all income received from the original increase in spending, or from successive doses of spending, is, in turn, spent. The marginal propensity to save, MPS or AS/∆Y, ensures that some income will be subtracted at every income period and withdrawn. Or, to put the matter another way, the increase in each successive round of spending will be determined by the marginal propensity to consume or consumption function (MFC or ∆C/ ∆Y) and this is less than 1. In this simplified economy with no government, as a matter of fact, income must either be spent on consumption or saved, so that
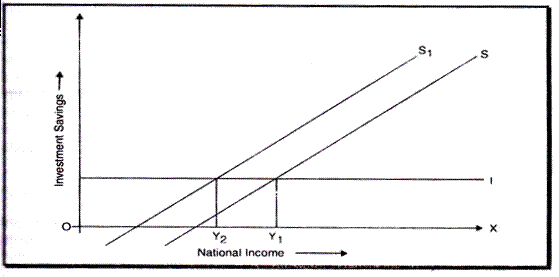
Instead of an increases in investment, let us assume that we get an increases in saving the upward shift in the saving schedule obviously gives rise to a contraction of national income as the new savings schedule cuts the investment schedule vertically above the investment schedule, vertically above Y2, indicating that the national income must, to reach a new equilibrium, fall from Y1 orY2. This is diagrammatically show in fig 3.
The decision to save more starts a contractive process, which in the end causes a drop in savings: savings and investment would be smaller at Y2 than at Y1. This is often referred to as the saving paradox.