Determination of National Income in Three-Sector Economy

The three-sector economy involves three sectors namely, households, business, and government.

The addition of the government in an economy results in bringing two variables in an economy. These variables are government expenditure (act as injections to income) and taxation (act as leakage or withdrawals from income).

In other words, the government expenditure increases the aggregate demand, while taxation reduces the aggregate demand.

Let us understand the effect of government expenditure and taxation on the level of national income assuming that the government is following a balanced budget policy. In such a case, the government expenditure (G) and government taxation (T) is equal.

The aggregate demand and aggregate supply in a three-sector economy can be determined as follows:

Aggregate Demand, AD = C + I + G

Aggregate Supply, AS = C + S + T

At the equilibrium point, AD = AS

C + S + T = C + I + G

Y = C + I + G

Where, C = a + bY_d

Y_d = Y – T

T = Lump-sum tax

Substituting the values of C and Y_d, we get the level of national income at equilibrium point:

Y = a + bY_d + I + G

Y = a + b(Y – T) + I + G

Y = a + bY – bT + I + G

Y (1-b) = a-bT + I + G

Y = 1/1-b (a -bT + I + G)

According to saving-investment approach, the national income can be determined with the help of the following formula:

C + S + T = C + I + G

C + S + T = C + I + G

S + T = I + G

Let us determine the level of national income by assuming consumption function as C = 100 + 0.75Y and I = 100. The government is following a balanced budget policy, according to which G = T= 50.

In such case, the national income at equilibrium point would be as follows:

Y = 1/1-b (a-bT + I + G)

Y = 1/10.75 (100 -0.75*50+ 100 + 50)

Y = 850

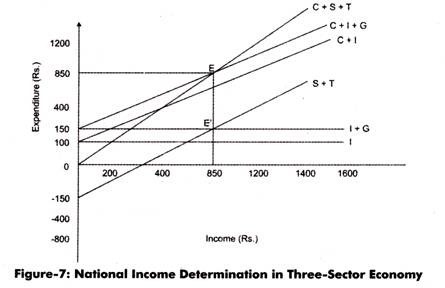
The graphical representation of determining national income in the three-sector economy is shown in Figure-7:

In Figure-7 C + S + T and C + I + G schedules intersect each other at point E. This the equilibrium point at which the national income is determined that is Rs. 850 in the present case. The S + T and I + G schedules also provide the same level of national income at equilibrium point E’.

Change in Government Expenditure and Government Expenditure Multiplier:

Let us determined the impact of change in government expenditure on the national income. Suppose that the government only purchases goods and services, while keeping the other variables at constant. The effect of change in government expenditure on national income is the same as the effect of change in autonomous investment. Increase in government expenditure is taken as ΔG that results in the increase of aggregate demand with the help of multiplier process.

The national income equilibrium can be determined with the help of following equation:

Y = 1/1-b (a – bT + I + G) (1)

Y + ΔY= 1/1-b (a – bT + I + G + ΔG) (2)

By subtracting equation (1) from (2), we get:

ΔY= 1/1-b (AG)

The government expenditure multiplier can be calculated by the following formula:

G_m = ΔY/ΔG = 1/1-b

Where G_m is the government expenditure multiplier.

Change in Lump Sum Tax and the Tax Multiplier:

The impact of change in lump-sum taxes on the national income is similar to the impact of government expenditure. Let us assume that the change in lump sum tax is ΔT and the resultant change in national income is ΔY.

In such a case, the national income equilibrium can be determined with the help of the following formula:

Y + ΔY = 1/1-b [a –b (T + ΔT) + I + G + ΔG]

Y + ΔY = 1/1-b [a – bT + bΔT + I + G + ΔG] (3)

By subtracting equation (1) from equation (3), we obtain:

ΔY= 1/1-b (-bΔT)

ΔY = bΔT/1-b

The tax multiplier (Tm) can be calculated by using the following equation:

T_m = ΔY/ΔT = -b/1-b

The tax multiplier contains a negative sign. This implies that increase in tax has an adverse or negative effect on national income.

As b = MPC and MFC <1, therefore

T_m = ΔY/ΔT = -b/1-b

In such a case, the tax multiplier is smaller than the government expenditure multiplier. Therefore, in case, the government expenditure is equal to increase in taxes (G =ΔT), then the national income would also increase.

Let us determine the increase occur in national income when G = ΔT with the help of balanced budget multiplier.

Balanced Budget Multiplier:

Till now we have discussed the change produced in national income due to government expenditure and taxes separately, while keeping the other variable at constant. Now, let us study the impact of change in government expenditure and taxes simultaneously on the national income. In this case, the change in government expenditure and taxes is of equal magnitude (ΔG = ΔT). Balanced budget policy is said to be implemented in a case when ΔG = ΔT.

The impact of balanced budget policy on national income is termed as balanced budget multiplier. According to balanced budget theorem, the numerical value of balanced budget multiplier is equal to one. Therefore, the theorem of balanced budget is also termed as unit multiplier theorem.

The numerical value of balanced budget multiplier can be derived with the help of equation (1), which is given as follows:

r = 1/1-b (a – bT + I + G)

The national income equilibrium after including the change in government expenditure (ΔG) and taxes (ΔT) along with the change produced in national income (ΔY) is as follows:

Y + ΔY = 1/1-b [a -bT + bΔT + I + G + ΔG] (4)

By subtracting equation (1) from equation (4), we get:

ΔY= 1/1-b (-bΔG + ΔG)

ΔY (1-b) = -bΔG + ΔG

ΔY (1-b) = ΔG (1-b)

ΔY = ΔG

The formula for calculating balanced budget multiplier (B_m) is as follows:

B_m = ΔY/ΔG = ΔG/ΔG

B_m = 1

Another method for calculating B_m is by adding up the G_m and T_m, described as follows:

B_m = G_m + T_m

B_m = 1/1-b + -b/1-b

B_m = 1

The value of balanced budget multiplier (B_m) is one. This implies that the change in national is exactly equal to the change in government expenditure and taxes simultaneously.

Proportional Income Tax and Balanced Budget Multiplier:

In the above, we have discussed the impact of lump-sumtax only on the national income. However, there is another type of tax, known as proportional tax. Proportional tax refers to a type of tax that is levied at the same rate, regardless of the amount earned by individuals. Now, let us analyze the effect of balanced budget and proportional income tax simultaneously on national income.

The tax function used for the analysis purpose is as follows:

T = T + tY

Where, T = Autonomous Tax

t = Proportion of income taxed

The following equation of national income equilibrium is used for the analysis purpose:

Y = a -b(Y – T) + I + G

By substituting the value of T in the national income equilibrium equation, we get:

Y – a-b [(Y – (T + tY)] + I + G

Y = a – bY – bT + btY + I + G

Y = 1/1-b+bt (a- bT + I + G)

Y = 1/1-b (1-t) (a- bT + I +G)

When the increase in government expenditure is ΔG, the increase in national income is ΔY.

The level of national income at this new equilibrium point is as follows:

Y + ΔY = 1/1-b (1-t) (a- bT + I + G + ΔG)

By subtracting equation (5) from equation (6), we get:

ΔY = 1/1-b (1-t) (ΔG)

The balanced budget multiplier with proportional tax is as follows:

ΔY/ΔG = 1/1 – b (1 – t)