Determination of National Income in an Open Economy

The Foreign Trade Multiplier:

David Hume was the first economist to suggest a connection between exports and imports, lie developed the price specie-flow mechanism to show how an increase in exports would lead to an increase in imports.

The mechanism, by which this operated, however, was not prices but changes in income. An increase in exports led to an increase in income, which in turn, operated to increased imports.

He believed that, the increase in imports would offset the original increase in exports. After the adjustment was complete, the BOP would be in balance. In fact, Hume appeared to believe that, before balance was finally reached, the export surplus would lead to an offsetting import surplus which would require the export of all gold previously imported on this account; it was not worthwhile attempting to achieve an export surplus and gold imports.

Hume’s law in international trade had its domestic parallel in Say’s law of markets. This held that a country could not have a depression due to under consumption because suppliers bringing goods to the market at the same time brought purchasing power. All goods brought to the market created sufficient purchasing power to buy all goods: every supply created its own demand. Parallel to Hume’s law that imports equal exports was Say’s law that purchases equal sales. Says law of markets was entirely satisfactory in a world of barter. In a monetary economy, however, the law did not hold because of the possibility that suppliers would return from the market bearing not goods but money.

In a monetary economy, income can be saved. The possibility of monetary savings undermines the rigorous equality between imports and exports implied by Hume’s law. Hume was right about international barter. But he was wrong about international trade conducted with monetary reserves. Let us explore the relations between national income and foreign trade.

The Import Function:

In a closed economy consumers could spend their income on consumption goods or they could save them. Total consumption could then be viewed as a function of the national income.

This functional relationship can be expressed in the following way:

C = C (Y)

Savings and consumption are both increasing functions of the national income. In an open economy, consumers will also demand imported goods, and imports can be expressed as a function of national income. We write the import function, as M = M (Y). Imports are also an increasing function of income.

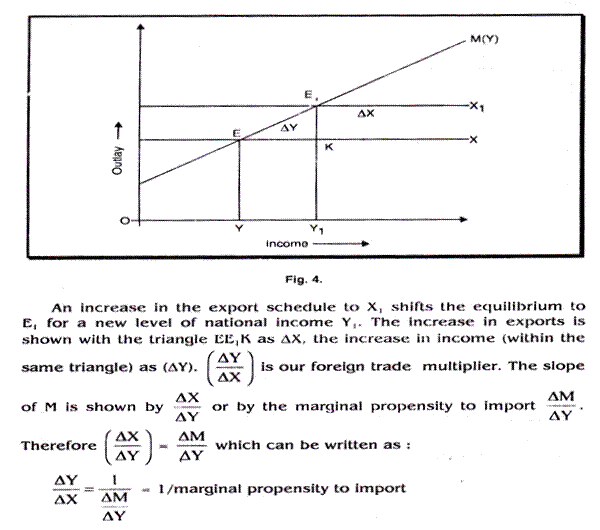
We can illustrate the import function graphically as shown in Fig. 4. The fig. shows that even at zero national income, something would be imported (by exporting part of the country’s capital stock or by borrowing abroad). As the national income increases, imports also Increase. A country’s average propensity to import is defined as the total imports divided by the total national income, that is, M/Y. The average propensity to import varies greatly between countries.

More important than the average propensity is the marginal propensity to import. This is the change in imports associated with a given change in income. Or the marginal propensity to import measures how much of a change in the national income is spent in Imports. In algebraic terms it is defined as ∆M/∆Y. If imports increase by 10 when the national income increases by 100, the marginal propensity to import will be 0.1.

If the marginal propensity to import is divided by the average propensity to import, we deduce the income elasticity of demand for imports. Expressed in algebraic terms this becomes — ∆M/∆Y/M/Y The income elasticity of imports is defined under the assumption that all other things are equal, for instance that there are no changes in prices. If the demand for imports increases by 5 percent when the income Increases by 10 percent, the income elasticity of imports equals 0 5. If a country’s average and marginal propensities to import are equal, its Income elasticity of demand for imports is 1.

This implies that as the country’s income increases, a constant proportion of the increasing Income is spent on imports, and the share of its national product which is traded is constant. If the marginal propensity to import is larger than its average propensity, this tends to increase the country’s independence on foreign trade, and if the opposite is the case, its foreign trade quota will fall.

Diagrammatic Analysis of the Open Economy: The Foreign Trade Multiplier where there is neither savings nor investment.

Let us assume an economy with no savings and no investment, and no government to tax or make public sector outlays. Then the goods produced Y plus imports M must be equal to goods bought C plus exports X and

Y _I M C _I X

But Y – C

Therefore M = X

In other words, exports are equal to imports at the equilibrium level of income Fig. 4 then shows the equilibrium position of income with given export and import schedules. Here, with a given import schedule M and a given export schedule X equilibrium will be at E for a level of national income OY.

Hence, the foreign trade multiplier K₁ is the reciprocal of the marginal propensity to import.

The lesson from this picture of a highly simplified economy is that any increase in exports produce such an increase in income as will increase imports and completely adjust the BOP.

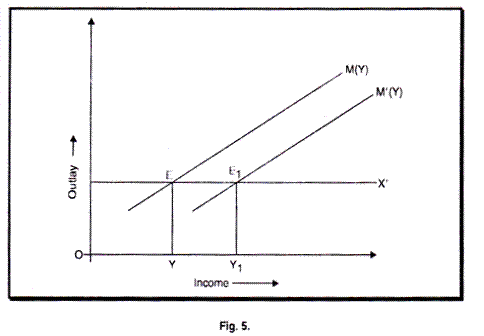
A shift in the propensity to import schedule will also change national income in this case. If exports remain unchanged at X but import function moves to M₁, so that at each level of income imports are less, the national income increases from OY to OY₁ as in Fig. 5. Such a shift of the import schedule might occur as a result of a change in tastes, or a redistribution of income or in relative prices.

A decline in propensity to import will lead to an increase in national income, while an increase in propensity to import will lead to a decline in national income.