Tax and National Income Determination (With Diagram)

We assumed that the government spends but doesn’t collect tax revenue. This means that the entire public expenditure is fi­nanced by deficit financing or money creation.

Now, let us assume that the government earns income in the form of tax revenue.

An increase in taxes reduces disposable in­come. Consumption now depends on after-tax income or disposable income.

Thus, taxes enter the model through the consumption function. Taxes are assumed to be exogenous. The basic equilibrium condition is the equality between aggregate supply and aggregate demand, i.e.,

Y = C + 1 + G

Or alternatively, leakages equal injections, i.e.,

S + T = 1 + G

As these two approaches are alternatives to each other here we consider the aggregate demand approach.

Aggregate demand approach suggests that equilibrium level of income is determined when aggregate demand equals aggregate value of output or aggregate supply. In this model, aggregate demand is affected by taxes. Taxes reduce disposable income.

Since con­sumption is a function of disposable income, an increase in taxes reduces consumption. Graphically, this means a downward shift in consumption function. Since consumption is a component of aggregate demand, aggregate demand schedule also shifts downward. Con­sequently, equilibrium level of income de­clines.

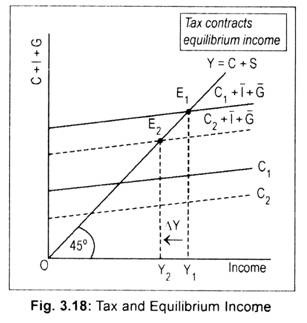
In Fig. 3.18, C₁ is the initial or pre-tax consumption function. As usual, private in­vestment and government expenditure are autonomous. By summing up the consumption schedule and autonomous investment and gov­ernment spending, we obtain pre-tax aggregate demand schedule (C₁ + I + g)- C₁ + I + g line cuts the 45° line at point E₁.

The correspond­ing level of national income is, thus, OY₁. Post- tax consumption line is C_r Since consumption line shifts downward following an increase in taxes, aggregate demand schedule now should shift to C₂ + I + G. The new equilib­rium level of income is OY₁, less than the ini­tial income level. Thus, an increase in taxes leads to a decline in national income. Or the effect of an increase in taxes on national in­come is contractionary.

Mathematical Example of Equilib­rium National Income Determination in a three-sector Economy:

Let the consumption function be

C = 70 + 0.9Y_d

(where Y_d = Y – T)

1 = 35, G = 20.

T = 0.2Y + 25

Now find the equilibrium values of na­tional income, consumption, disposable in­come, tax.

Solution:

Putting the values of C, I, G and T, we get