One of the major assumptions underlying the properties of isoquants is that the inputs, X and Y, are continuously, but not perfectly, substitutable. As the firm goes on substituting X for Y, or the other way round, the marginal rate of technical substitution (MRTS) diminishes monotonically.
However, in the case of some production functions, we may see that the MRTSX,Y while diminishing, may become equal to zero at some point, because no more of Y can be given up for having more of X. Thereafter, as x rises, y also would have to rise to correct the mismanagement caused by the presence of excessive quantities of input X, and perhaps at an increasing rate.
All this implies that the slope of an IQ would be zero at some point (where MRTSX,Y = 0) and then the IQ would be positively sloped and convex downwards.
Similarly, MRTSX,Y, while diminishing as y increases, may become equal to zero, i.e., MRTSX,Y may become equal to infinity, at some point. Thereafter, as y rises, x also would have to rise, and perhaps at an increasing rate.
ADVERTISEMENTS:
All this implies that the slope of an IQ would become infinity as some point (where MRTSX,Y = 0 or MRTSX,Y = ∞), and then the IQ would be positively sloped and it would be concave downwards.
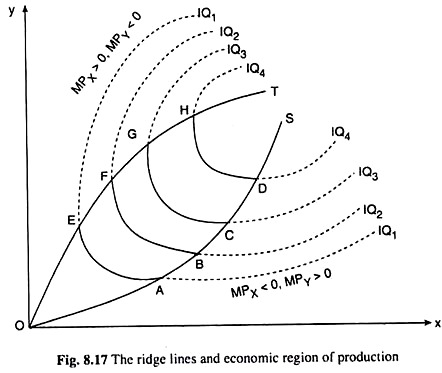
We have shown the IQ map for such a production function in Fig. 8.17, where we have constructed only four IQs. For any of these IQs, say for IQ1, we may observe the following:
(i) At some point like A, the slope of IQ1 is zero, i.e., MRTSX,Y = 0 and the IQ is horizontal.
(ii) At some point like E, the slope of IQ, = i.e., MRTSX,Y = ∞ or MRTSY,X = 0, and the IQ is vertical.
ADVERTISEMENTS:
(iii) In between the points A and E, IQ1 is negatively sloped and convex to the origin.
(iv) To the right of the point A, IQ1 is convex downwards, and to the right of the point E, IQ1 is concave downwards.
If we join the point of origin O and the points like A, B, C, D, etc. where MRTSX,Y = 0, by a line like OS in Fig. 8.17, we obtain what is known as a ridge line. Similarly, if we join the point O and the points like E, F, G, H, etc., where MRTSX,Y = by a line like OT, we obtain another ridge line.
ADVERTISEMENTS:
Let us note that OS is called the lower ridge line and OT is called the upper ridge line. Let us also note that at each point on the lower ridge line, MRTSX,Y = 0 and at each point on the upper ridge line, MRTSX Y = ∞. Lastly, let us note that the ridge lines separate the negatively sloped portion of an IQ from its positively sloped portions.
We have discussed above about the positively sloped portions of IQs that some production functions may give rise to. But the firm would prima facie reject these positively sloped portions as uneconomic.
This is because along these portions the firm uses more of both the inputs, but the output does not increase, it remains constant. Therefore, a profit-maximising firm purchasing the inputs at positive prices, would summarily reject the positively sloped portions as irrelevant.
Now, what can we say about this irrelevance in terms of marginal productivity (MP) of the inputs. Along the positively sloped portions below the lower ridge line, as x increases, y remaining constant, the firm would move from a higher IQ to a lower IQ, i.e., here MPX would be obtained to be negative.
On the other hand, if the firm increases y, x remaining constant, it would move from a lower IQ to a higher IQ, i.e., here MPY would be positive. Similarly, we would find that along the positively sloped portions above the upper ridge line, MPX would be positive and MPY would be negative. Since the MP of one of the inputs is negative along the positively sloped portions, the firm would consider the region as uneconomic.
But, the negative slope of an IQ has been obtained on the basis of the assumption that both the inputs have positive MPs. This is apparent in Fig. 8.17 also. Along the negatively sloped portions, as the firm increases x, y remaining constant, it moves from a lower to a higher IQ, i.e., here MPX would be positive.
Similarly, here MPY would also be positive. So the negatively sloped portions of IQs form the economic region of the production function. The firm would select some point (input combination) in this region where it can produce a given quantity of output at the lowest possible cost.