How to Calculate Production Function?

A function represents a relationship between two variables.

For example, variable X and variable Y are related to each other in such a manner that a change in one variable brings a change in the other.

 “Production Function is the technological relationship which explains the quantity of production that can be produced by a certain group of inputs. It is related with a given state of technological change”-Samuelson.

The relationship between X and Y can be shown with the help of a formula, which is shown as follows:

Y = f(X)

In the aforementioned formula, the value of Y can be determined with the help of the given value of X. Similarly, production function is the mathematical representation of relationship between physical inputs and physical outputs of an organization.

In other words, production function represents the maximum output that an organization can attain with the given combinations of factors of production (land, labor, capital, and enterprise) in a particular time period with the .given technology. It acts as a collection of different production possibilities of an organization.

Some of the popular definitions of production function are as follows:

In the words of Prof. Leftwitch, “The term Production function is used to explain the physical relationship between the units of the factors of production of a firm (inputs) and the units of goods and services obtained per unit of time (outputs).”

According to Citowiski, “Production of a firm is the function of factors of production. If it is presented mathematically, it is called Production Function.”

According to Samuelson, “Production Function is the technological relationship which explains the quantity of production that can be produced by a certain group of inputs. It is related with a given state of technological change.”

In the words of Watson, “The relation between a firm’s physical production (output) and the material factors of production (input) is referred to as production function.”

The relationship between input and output is represented in the form of table, graph, or equation. The input-output relationship is presented in a quantitative form.

The long-run production function (Q) is usually expressed as follows:

Q = f (LB, L, K, M, T, t)

Where, LB= land and building

L = labor

K = capital

M = raw material

T = technology

t = time

However, the production function has reduced to capital and labor, so that it can be easily understood.

A two variable production function can be expressed as follows:

Q = f (L, K)

Other factors are excluded from the production function due to various reasons. Land and building are excluded because they are constant for aggregate production function. However, in case of individual production function, they are included in capital factor Raw materials are excluded because they represent a constant relationship with the output at all phases of production.

For example steel, tires, steering, and engines used for manufacturing cars explains a constant relationship with the number of cars. Similarly’ time and technology are also constant over a period of time.

The algebraic or equation form of production function is most commonly used to analyze production. Let us understand the algebraic form of production function with the help of an example. Suppose a diamond mining organization has used two inputs capital and labor in the production of diamonds.

Therefore, its production function can be expressed as under:

Q = f (L, K)

Where, L = labor

K = capital

This production function implies that quantity of diamond production depends on labor engaged in producing diamond and capital required to carry out production. The production of diamonds would increase with the increase in labor and capital. On the basis of time period required to increase production, an organization decides whether it should increase labor or capital or both.

An organization takes into account either long- run production or short-run production for increasing the level of production. In short-run, the supply of capital is inelastic (except for individual organization in perfect competition). This implies that capital is constant. In such a case, the organization only increases labor to increase the level of production.

On the other hand, in the long- run, the organization can increase labor and capital both for increasing the level of production. Therefore, on the basis of time period, production function can be classified in two types, namely, short-run production function and long-run production function.

The short-run production function can be mathematically expressed as follows:

Q = f (L, K)

= constant

For example, if a production function is as follows:

Q = bL

In this case, b is the constant return to labor, which can be calculated as follows:

b = ∆Q/∆L

On the other hand, the long-run production function can be algebraically represented as follows:

Q = f (L, K)

Let us convert the equation of production function into a table of production function with the help of Cobb-Douglas production function.

The equation of Cobb-Douglas production function is as follows:

Q = ∆K ^aL^b

Where, A, a, b = parameters

K= capital

L = labor

Q = maximum quantity of commodity

b= 1-a

For example, the values of parameters A, a, and b is 50, 0.5, and 0.5, respectively.

In such a case, the production function can be expressed as follows:

Q = 50K ^0.5L^0.5

This production function can be used to determine value of Q when the combination of K and L are different.

The value of Q can be determined with the help of the following formula:

Q = 50 √KL

Or,

Q = 50 √K √L

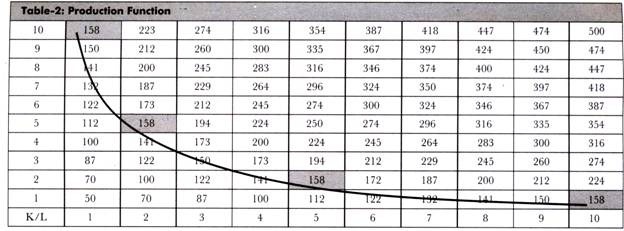
Suppose, K= 2 and L= 5, then the value of Q is as follows:

Q = 50 √2 √5

Q = 158

Similarly, the value of Q can be determined for different values of K and L.

These values can be represented in the form of a table that is known as tabular form of production function, which is shown in Table-2:

In Table-2, it can be seen that there are four combinations of K and L, which are yielding the same value of Q, 158. On joining these four combinations, a curve is drawn known as isoquant.