Compatibility between the Concepts of Constant Returns to Scale and Diminishing Returns to a Factor:
It is quite conceivable that a production function may possess the properties of constant returns to scale in the long run, i.e., the production function may be homogeneous of degree one. For we may imagine that when all the inputs are doubled or trebled, the whole production system may be considered to have been duplicated—or triplicated—and so the output of the firm may very well be doubled or trebled.
But if, in this production function, we vary only a single factor (say, labour), keeping all other factor quantities constant, then the returns to the factor (labour) would be eventually diminishing—initially, the returns to the factor may be increasing or constant. As we know whether the returns would be increasing, constant or diminishing, depends upon the proportion between the variable factors and the fixed factors.
We may also see in a simple way with the help of a diagram that if the returns to scale are constant, then the returns to a single factor would be diminishing. In Fig. 8.27 we have assumed that the firm uses only two factors, labour (L) and capital (K) to produce a single output, and the production is subject to constant returns to scale (in the long run).
ADVERTISEMENTS:
That is why the expansion path, OR, of the firm has been a straight line. It can be seen in Fig. 8.27 that when the firm doubles the quantity used of L and K and moves from the point E to the point F on its expansion path (OE = EF, or, OF = 2.0E), the quantity of output has doubled from 10 units to 20 units.
Again, when the firm trebles the quantities of the inputs and moves from the point E to the point G (OG = 3.0E), the quantity of output has trebled from 10 to 30 units. From Fig. 8.27, it is evident that whenever the firm increases L at a rate of EM and K at a rate of FM, its output would increase at a constant rate of 10 units. Thus, by increasing L and K at the said rates, the firm comes from the point E to the point F and output (Q) rises by 10 units.
Again, when at point F, the firm increases L and K at the rates FP (= EM) and GP (= FM), its output again rises by 10 units (from 20 to 30), and the firm moves from point F to point G on its expansion path.
But, if at the point F, the firm’s quantity of capital (K) becomes fixed at K = K̅, and labour quantity (L) remains variable, then the firm can increase its output by 10 units (from 20 to 30) only if it increases L by FN—only then the firm can move from the point F to the point N on IQ3 (Q = 30).
ADVERTISEMENTS:
But from Fig. 8.27, it is obvious that FN > FP (= EM). That is, we have obtained that if K becomes fixed, then in order to increase its output at a constant rate (of 10), the firm would have to increase L at a higher rate (FN > EM).
In other words, if the firm increases only the use of the variable factor, labour, at a certain rate (here EM), its output would rise at a smaller rate, i.e., the returns to the variable factor, L, would be diminishing.
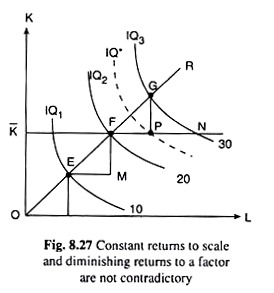
In Fig. 8.27, we see that if at F, the firm increases L at the rate of FP (= EM), K remaining fixed, then it would move from the point F on IQ2 to the point P on IQ* which is a lower IQ than IQ3 (Q = 30). We may conclude from above that diminishing returns to a variable factor (in the short run) are not inconsistent with constant returns to scale in the long run.