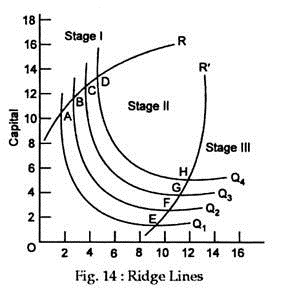
The below mentioned article provides a short note on ridge lines. This will also help you to draw the diagram of ridge lines.
The marginal product of a particular factor may be negative if the quantity used is too large. For example, if too much labour is used there may be congestion and the efficiency of all the labourers may be affected. An isoquant will include points denoting such factor quantities, because it includes all factor combinations producing the same output.
But, a rational producer will not operate on this part of the isoquant. The area of rational operation may be shown by drawing two lines from the origin enclosing only those parts of the isoquants where each factor has a positive marginal product. Such lines are called ridge lines. Negative marginal products appear in that part of the isoquant which has a positive slope.
Ridge lines exclude these parts. This can be seen in Fig. 14. Let us focus our attention on isoquant Q1 over the interval from point A to point E. We now know that as we substitute labour for capital and move from A toward E, the marginal productivity of labour diminishes.
But, look what happens if we move beyond E, continuing to use more labour. The isoquant Q1 turns upward, indicating that if we use more labour and still want to produce Q1 units, we must now also use more capital. Why? Because beyond E, the marginal product of labour has become negative, and so to compensate for using more labour, we must add to the amount of capital used as well.
If we follow Q2, Q3 or Q4 from left to right, we see that a similar result occurs. Beyond points F, G and H turn up. That is, the slopes of the isoquants become positive due to the negative marginal productivity of labour.
The line (R’) connecting all points, such as £, F, G and H, is called a ridge line; it marks off the boundary between stage II and stage III of production. No one would want to produce in stage III, since the same level of production could be obtained with fewer of both inputs by moving to the left along the appropriate isoquant until stage II was reached.
ADVERTISEMENTS:
We can now apply this same line of reasoning to rule out stage I. Again let us concentrate attention on isoquant Q1. This time, suppose we move up and to the left toward point A. As we do so, substituting capital for labour, the marginal productivity of capital diminishes and becomes negative if we go beyond A. Thus, if we add more capital above A while maintaining output at the Q1 level, we must use more labour.
This does not make much sense from a managerial perspective. Points B, C and D are analogous to point A for their respective isoquants. Beyond these points, the marginal productivity of capital is negative and so we would not wish to operate in that region, which we refer to as stage I.
The ridge line R marks the boundary between stage I and stage II just as R’ marks the boundary between stages II and III. We see that neither stage I nor stage III is desirable for production, since the marginal productivity of at least one input is negative in those stages. We can then conclude that the only relevant region for production is stage II, which is bounded by the two ridge lines, R1 and R2. This region is called the economic region of production.