Law of Returns to Scale : Definition, Explanation and Its Types!
In the long run all factors of production are variable. No factor is fixed. Accordingly, the scale of production can be changed by changing the quantity of all factors of production.
Definition:
“The term returns to scale refers to the changes in output as all factors change by the same proportion.” Koutsoyiannis
“Returns to scale relates to the behaviour of total output as all inputs are varied and is a long run concept”. Leibhafsky
ADVERTISEMENTS:
Returns to scale are of the following three types:
1. Increasing Returns to scale.
2. Constant Returns to Scale
3. Diminishing Returns to Scale
Explanation:
In the long run, output can be increased by increasing all factors in the same proportion. Generally, laws of returns to scale refer to an increase in output due to increase in all factors in the same proportion. Such an increase is called returns to scale.
ADVERTISEMENTS:
Suppose, initially production function is as follows:
P = f (L, K)
Now, if both the factors of production i.e., labour and capital are increased in same proportion i.e., x, product function will be rewritten as.
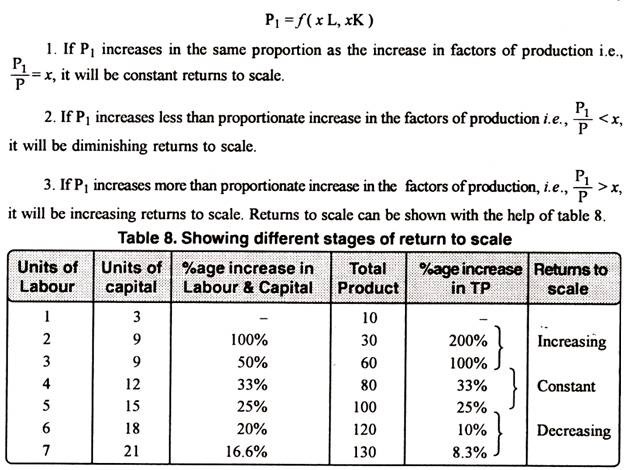
The above stated table explains the following three stages of returns to scale:
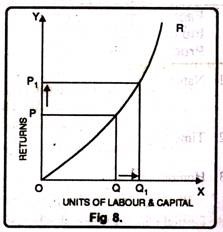
1. Increasing Returns to Scale:
Increasing returns to scale or diminishing cost refers to a situation when all factors of production are increased, output increases at a higher rate. It means if all inputs are doubled, output will also increase at the faster rate than double. Hence, it is said to be increasing returns to scale. This increase is due to many reasons like division external economies of scale. Increasing returns to scale can be illustrated with the help of a diagram 8.
In figure 8, OX axis represents increase in labour and capital while OY axis shows increase in output. When labour and capital increases from Q to Q1, output also increases from P to P1 which is higher than the factors of production i.e. labour and capital.
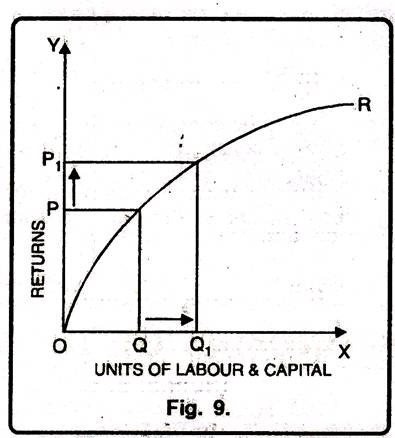
2. Diminishing Returns to Scale:
Diminishing returns or increasing costs refer to that production situation, where if all the factors of production are increased in a given proportion, output increases in a smaller proportion. It means, if inputs are doubled, output will be less than doubled. If 20 percent increase in labour and capital is followed by 10 percent increase in output, then it is an instance of diminishing returns to scale.
The main cause of the operation of diminishing returns to scale is that internal and external economies are less than internal and external diseconomies. It is clear from diagram 9.
In this diagram 9, diminishing returns to scale has been shown. On OX axis, labour and capital are given while on OY axis, output. When factors of production increase from Q to Q1 (more quantity) but as a result increase in output, i.e. P to P1 is less. We see that increase in factors of production is more and increase in production is comparatively less, thus diminishing returns to scale apply.
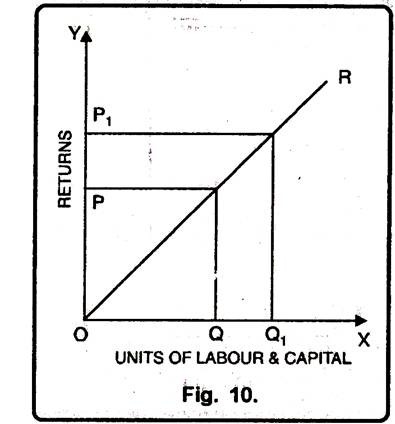
3. Constant Returns to Scale:
Constant returns to scale or constant cost refers to the production situation in which output increases exactly in the same proportion in which factors of production are increased. In simple terms, if factors of production are doubled output will also be doubled.
In this case internal and external economies are exactly equal to internal and external diseconomies. This situation arises when after reaching a certain level of production, economies of scale are balanced by diseconomies of scale. This is known as homogeneous production function. Cobb-Douglas linear homogenous production function is a good example of this kind. This is shown in diagram 10. In figure 10, we see that increase in factors of production i.e. labour and capital are equal to the proportion of output increase. Therefore, the result is constant returns to scale.
ADVERTISEMENTS: