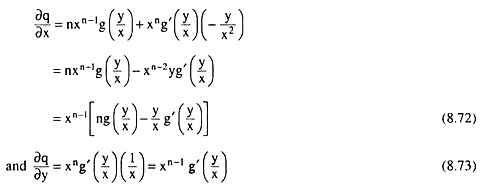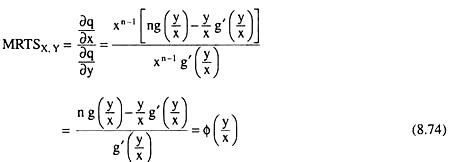Isoclines are obtained from the production function, say, q = f(x, y) of the firm. An isocline is a curve that starts from the origin and passes through the isoquant map of the firm, and along which the marginal rate of technical substitution of input X for input Y, i.e., the numerical slope of the isoquants is constant. Therefore, the equation of an isocline is
MRTSX,Y = Constant (8.66)
(8.66) gives us that we may have a large number of isoclines for the firm’s production function depending on the value of the constant on the right hand side. If this constant is the ratio of the prices of the inputs, i.e., rX/rY = constant, then the isocline is actually the expansion path of the firm, the equation of this path being
MRTSX,Y = rX/rY = Constant (8.67)
ADVERTISEMENTS:
Again, if this constant is either zero or infinity, then the isocline is, respectively, the lower or the upper ridge line, their equations being
MRTSX,Y = 0 (8.68)
and MRTSX,Y = ∞ (8.69)
We have given above the definition of isoclines and we have to remember that the expansion path of the firm and the ridge lines are also isoclines.
ADVERTISEMENTS:
Isoclines under Homogeneous Production Function:
The isoclines associated with a homogenous production function are straight lines. This we can prove as follows.
Let us suppose that the production function of a firm is
ADVERTISEMENTS:
q = f(x, y) [(8.21)]
If (8.21) is a homogeneous function of degree n, we have
Where t is any positive real number. Now putting t = 1/x in (8.70), we have
Now from (8.71), we have:
Therefore, from (8.72) and (8.73), we have
But, by definition, the numerical slope of the IQs or the MRTSx,y along an isocline is constant. Therefore, from (8.74), we have
(8.75) gives us that, in the case of a homogeneous production function of any degree n, the isoclines are Straight lines. We may also conclude, therefore, that the expansion path of the firm and the ridge lines are also straight lines under homogeneous production function of any degree n, since they are isoclines.