In this article we will discuss about the demand and supply curve of labour of a firm in perfect competition.
All profit-maximising firms will hire units of the variable factor up to the point at which the marginal cost of the factor equals the marginal revenue that is produced by the factor. For a firm that is a price taker in factor markets, this means that it hires a factor up to the point at which the factor’s price equals its marginal revenue product.
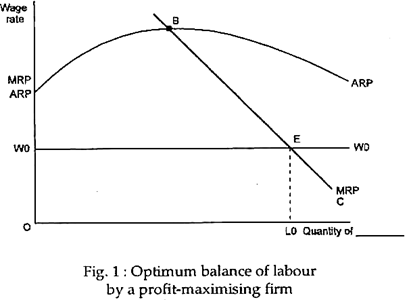
Consider a single firm with only one variable factor, labour, and one fixed factor, capital. Assume that the average and marginal revenue products of the labour are those shown in Fig. 1. The firm wishes to hire the quantity of labour that will maximise its profits.
The demand curve for a factor is the downward-sloping portion of the marginal revenue product curve where it is below the average revenue product curve. To see why this statement is correct, let us first ask a number of questions.
ADVERTISEMENTS:
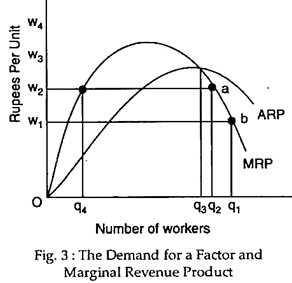
Why do points on the downward sloping portion of MRP, such as a and b in Fig. 3 belong on the demand curve? If the wage rate (the price of the variable factor) is w2, the profit-maximising firm will hire the factor up to the point where w – MRP, that is, up to q2. This is point a. If the wage rate is W1, the firm will hire up to q2. This is point b. Points a and b are thus on the firm’s demand curve for the factor.
What is the maximum wage rate that the firm will pay? It will never be worthwhile for the firm to produce a product when its price is below the level of average variable cost.
ADVERTISEMENTS:
Where average product is a maximum, average variable cost is a minimum. For any wage rate above to w3, such as w4, the average revenue that is generated by a unit of labour (shown by ARP) would be less than the variable cost of that unit of labour (its wage rate). For such a wage rate it is not worthwhile for the firm to hire any workers. In other words, w3, where average revenue product is a maximum, is the highest factor price that a firm could pay and still cover its variable costs.
Why is the downward sloping, not the upward sloping, portion of MRP the demand curve? Consider the wage rate w2. Here, w = MRP at both q4 (point c) and q2 (point a). Here, point a is on the demand curve, what about point c? For every unit/labour that is hired up to q4, MRP is less than the wage rate. In other words, each unit of labour is contributing less to revenue than to cost.
Thus, a profit-maximising firm would be better off if it hired zero units rather than q4 units. For every unit of labour from q4 to q2, MRP exceeds the wage rate. Thus, if a firm were hiring q4 units, it would find each additional unit beyond q4 (up to q2) worth hiring. Point c, where MRP is rising when it equals the wage rate, a point of minimum profit, not maximum profit.
A firm at point c would improve its profitability by moving in either direction—to hiring zero workers or to hiring q2 workers. (We already know that q2 is better than zero, because at that quantity ARP is greater than the wage rate) Only points where MRP cuts the wage rate from above, that is, where MRP is downward sloping, are possible profit-maximising quantities.
ADVERTISEMENTS:
Downward Slope of MRP:
We may now ask, having shown that only downward sloping portions of MRP are relevant to the demand curve for the factor, whether we have any reason to believe that MRP will slope downward. The presence of diminishing returns is sufficient to assure this result, as we can easily show.
Marginal revenue product depends on two things:
(1) The physical increase in output that an additional unit of the variable factor makes possible and
(2) The increase in revenue derived from that extra output.
The first of these is called the marginal product (MP); the second of these is called marginal revenue.
MRP = MP x MR
The hypothesis of diminishing marginal returns was introduced. This hypothesis says that MP has a declining section over some range of output. If marginal revenue is constant (as it is in perfect competition), MRP will have the same shape as MP and must also decline.
Marginal revenue, however, may not be constant. If MR declines as output increases (as it does in monopoly and in any other situation in which the firm’s demand curve declines), MRP must decline even more sharply. The hypothesis of diminishing marginal productivity thus implies diminishing MRP and a downward sloping demand curve for the factor.