Returns to Scale and Returns to Factor (With Diagram)

In this article we will discuss about the relationship between Returns to Scale and Returns to Factor.

Returns to a factor and returns to scale are two important laws of production. Both laws explain the relation between inputs and output. Both laws have three stages of increasing, decreasing and constant returns. Even then, there are fundamental differences between the two laws.

Returns to a factor relate to the short period production function when one factor is varied keeping the other factor fixed in order to have more output, the marginal returns of the Variable factor diminish. On the other hand, returns to scale relate to the long period production function when a firm changes its scale of production by changing one or more of its factors.

Assumptions:

We discuss the relation between the returns to a factor (law of diminishing returns) and returns to scale (law of returns to scale) on the assumptions that:

(1) There are only two factors of production, labour and capital.

(2) Labour is the variable factor and capital is the fixed factor.

(3) Both factors are variable in returns to scale.

(4) The production function is homogeneous.

Explanation:

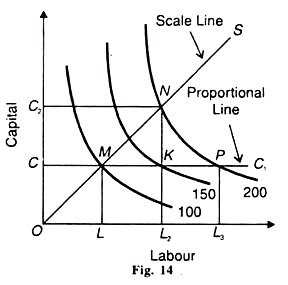
Given these assumptions, we first explain the relation between constant return to scale and returns to a variable factor in terms of Figure 14 where OS is the expansion path which shows constant returns to scale because the difference between the two isoquants 100 and 200 on the expansion path is equal i.e.,

OM = MN. To produce 100 units, the firm uses ОС + OL quantities of capital and labour and to double the output to 200 units, double the quantities of labour and capital are required so that ОС₂ + OL₂ lead to this output level at point N. Thus there are constant returns to scale because OM = MN.

To prove that there are decreasing returns to the variable factor, labour, we take ОС of capital as the fixed factor, represented by the CC line which is parallel to the X-axis relating to labour.

This is called the proportional line. Keeping С as constant, if the amount of labour is doubled by LL₂ we reach point Y which lies on a lower isoquant 150 than the isoquant 200. By keeping С constant, if the output is to be doubled from 100 to 200 units, then OL₃ units of labour will be required. But OL₃ > OL₂. Thus by doubling the units of labour from OL to OL₂ with constant C the output less than doubles.

It is 150 units at point K instead of 200 units at point P. This shows that the marginal returns of the variable factor, labour, have diminished when there are constant returns to scale.

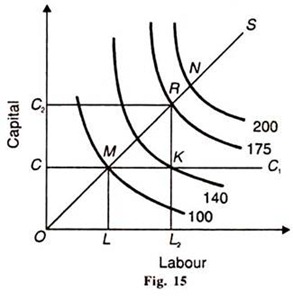
The relation between diminishing returns to scale and returns to a variable factor is explained with the help of Figure 15 where OS is the expansion path which depicts diminishing returns to scale because the segment MN > OM. It means that in order to double the output from 100 to 200, more than double the amounts of both factors are required.

Alternatively, if both factors are doubled to ОС₂ + OL₂, they lead to the lower output level isoquant 175 at point R than the isoquant 200 which shows diminishing returns to scale. If С is kept constant and the amount of variable factor, labour, is doubled by LL₂, we reach point K which lies on a still lower level of output represented by the isoquant 140. This proves that the marginal returns of the variable factor, labour, and have diminished when there are diminishing returns to scale.

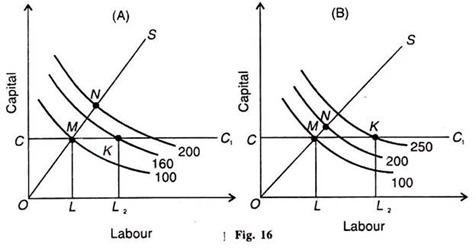
Now we take the relation between increasing returns to scale and returns to a variable factor. This is explained in terms of figure 16 (A) and (B) In Panel (A), the expansion path OS depicts increasing returns to scale because the Segment ОМ > MN. It means that in older to double the output from 100 to 200 less than double the amounts of both factors will be required.

If С is kept constant and the amount of variable factor labour is doubled by LL₂ the level of output is reached at point K which shows diminishing marginal return as represented by the lower isoquant 160 than the isoquant 200 when returns to scale are increasing.

In case the returns to scale are increasing strongly, that is, they are highly positive; they will offset the diminishing marginal returns of the variable factor, labour. Such a situation leads to increasing marginal returns. This is explained in Panel (B) of Figure 16 where on the expansion path OS the segment OM > MN, thereby showing increasing returns to scale.

When the amount of the variable factor, labour, is doubled by LL while keeping С as constant, we reach the output level K represented by the isoquant 250 which is at a higher level than the isoquant 200. This shows that the marginal returns of the variable factor, labour, have increased even when there are increasing returns to scale.

Conclusion:

It can be concluded from the above analysis that under a homogeneous production function when a fixed factor is combined with a variable factor, the marginal returns of the variable factor diminish when there are constant, diminishing and increasing returns to scale. However, if there are strong increasing returns to scale, the marginal returns of the variable factor increase instead of diminishing.