Imposition of Lump-Sum Taxes in Monopoly | Markets

In this article we will discuss about the imposition of lump-sum taxes in monopoly.

Monopolies may be regulated by means of imposition of lump-sum taxes. Since a lump-sum tax is like a fixed cost to a monopolist, its imposition will result in an upward shift of his total cost (TC) curve by a vertical distance equal to the amount of the tax.

Since the slope of the post-tax TC curve at each output would be the same as that of the pre-tax TC curve, the MC curve of the monopolist would remain unaffected by the tax. As a result, his equilibrium point and the equilibrium price-output combination would also remain unaffected by the tax.

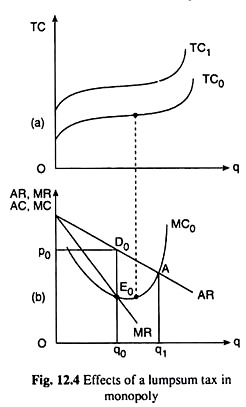
In Fig. 12.4(a), initially the (short-run) TC curve of the monopolist is TC₀ and the corresponding MC curve (short-run) is MC₀. The MR = MC equilibrium point of the monopolist is E₀ and his equilibrium price-output combination is D₀ (p₀, q₀) on his AR curve. At this point, the monopolist would sell q₀ of output at the price = p₀.

Let us now assume that a lump-sum tax of the amount T is imposed on the monopoly-firm. As a result, the TC curve of the monopolist would shift upwards from TC₀ to TC₁, the vertical gap between these two curves being equal to the amount of the tax, T.

However, after the imposition of the tax, the MC curve would remain the same as MC₀ and the equilibrium price-output combination would remain the same as D₀ (p₀, q₀).

However, since TC is larger at each q after the imposition of the tax, the difference between the monopolist’s total revenue and total cost, i.e., his profit would now fall, causing a redistribution of incomes. It may be noted also that the welfare cost of monopoly would remain unaffected by the imposition of the lump-sum tax.

In Fig. 12.4(b) it would remain unchanged, being equal to area AD₀E₀. For, under monopoly, output would be less than the p = MC output by q₁ – q₀, and the aggregate p – MC loss will be equal to □AD₀E₀.

Per-Unit Excise Tax in Monopoly:

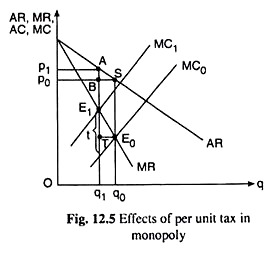
Per-unit excise tax is imposed on the basis of per-unit of the product. Unlike a lump-sum tax, a per-unit tax in monopoly causes an upward shift in the monopolist’s average cost (AC) and marginal cost curves, by the amount of the tax, say, t. Consequently, the equilibrium output of the monopolist will fall and the price will rise. This has been shown in Fig. 12.5.

In Fig. 12.5, initially, the marginal cost curve of the monopolist is MC₀ and this curve, after the imposition of the tax, is MC₁, the vertical gap between the two curves being t. Therefore, the equilibrium point of the monopolist will move from E₀ or S(p₀, q₀) to E₁ or A(p₁, q₁), q₁ < q₀ and p₁ > p₀.

Let us also note that although the price will increase as a result of the imposition of the per- unit tax, it will increase by less than the amount of the tax. We can easily prove this in the following way with the help of Fig. 12.5, where all the AR, MR, and MC curves have been assumed to be straight lines.

In Fig. 12.5, as the tax is imposed, the movement along the negatively sloped MR curve from the initial equilibrium (MR = MC) point, E₀, on MC₀, to the post-tax equilibrium point E₁ on MC₁ results in a rise in both MR and MC by the amount E₁T which is less than the amount of the tax t.

Now, since the numerical slope of the AR curve is equal to half of that of the MR curve, we have AB/BS = ½ 1E₁T/2TE₀ which gives us AB = 1/2E_tT (BS = TE₀), i.e., the rise in the price (= AB) is less than the rise in MR (= E₁T) which, in its turn, is less than t, i.e., the tax causes the price to rise by less than the amount of the tax (t).