A. Short-run equilibrium:
The monopolist maximizes his short-run profits if the following two conditions are fulfilled Firstly, the MC is equal to the MR.
Secondly, the slope of MC is greater than the slope of the MR at the point of intersection.
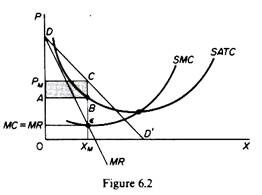
In figure 6.2 the equilibrium of the monopolist is defined by point ɛ, at which the MC intersects the MR curve from below. Thus both conditions for equilibrium are fulfilled. Price is PM and the quantity is XM. The monopolist realizes excess profits equal to the shaded area APM CB. Note that the price is higher than the MR.
In pure competition the firm is a price-taker, so that its only decision is output determination. The monopolist is faced by two decisions: setting his price and his output. However, given the downward-sloping demand curve, the two decisions are interdependent.
ADVERTISEMENTS:
The monopolist will either set his price and sell the amount that the market will take at it, or he will produce the output defined by the intersection of MC and MR, which will be sold at the corresponding price, P. The monopolist cannot decide independently both the quantity and the price at which he wants to sell it. The crucial condition for the maximization of the monopolist’s profit is the equality of his MC and the MR, provided that the MC cuts the MR from below.
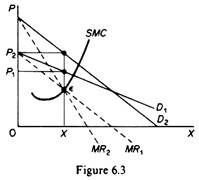
We may now re-examine the statement that there is no unique supply curve for the monopolist derived from his MC. Given his MC, the same quantity may be offered at different prices depending on the price elasticity of demand. Graphically this is shown in figure 6.3. The quantity X will be sold at price P1 if demand is D1, while the same quantity X will be sold at price P2 if demand is D2.
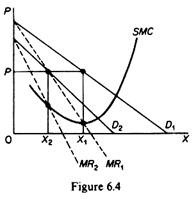
Thus there is no unique relationship between price and quantity. Similarly, given the MC of the monopolist, various quantities may be supplied at any one price, depending on the market demand and the corresponding MR curve. In figure 6.4 we depict such a situation. The cost conditions are represented by the MC curve. Given the costs of the monopolist, he would supply 0X1, if the market demand is D1, while at the same price, P, he would supply only 0X2 if the market demand is D2.
B. long-run equilibrium:
In the long run the monopolist has the time to expand his plant, or to use his existing plant at any level which will maximize his profit. With entry blocked, however, it is not necessary for the monopolist to reach an optimal scale (that is, to build up his plant until he reaches the minimum point of the LAC). Neither is there any guarantee that he will use his existing plant at optimum capacity. What is certain is that the monopolist will not stay in business if he makes losses in the long run.
ADVERTISEMENTS:
He will most probably continue to earn supernormal profits even in the long run, given that entry is barred. However, the size of his plant and the degree of utilization of any given plant size depend entirely on the market demand. He may reach the optimal scale (minimum point of LAC) or remain at suboptimal scale (falling part of his LAC) or surpass the optimal scale (expand beyond the minimum LAC) depending on the market conditions.
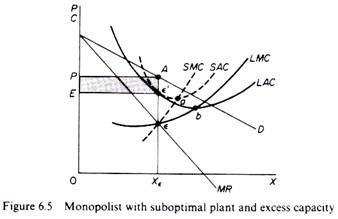
In figure 6.5 we depict the case in which the market size does not permit the monopolist to expand to the minimum point of LAC. In this case not only is his plant of suboptimal size (in the sense that the full economies of scale are not exhausted) but also the existing plant is underutilized. This is because to the left of the minimum point of the LAC the SRAC is tangent to the LAC at its falling part, and also because the short-run MC must be equal to the LRMC. This occurs at e, while the minimum LAC is at b and the optimal use of the existing plant is at a. Since it is utilized at the level e’, there is excess capacity.
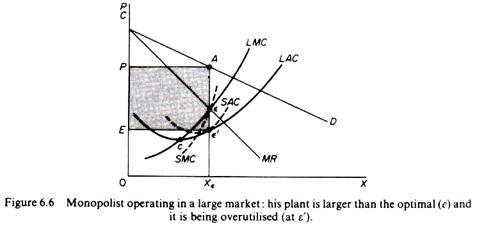
In figure 6.6 we depict the case where the size of the market is so large that the monopolist, in order to maximize his output, must build a plant larger than the optimal and overutilise it. This is because to the right of the minimum point of the LAC the SRAC and the LAC are tangent at a point of their positive slope, and also because the SRMC must be equal to the LAC. Thus the plant that maximizes the monopolist’s profits leads to higher costs for two reasons firstly because it is larger than the optimal size, and secondly because it is overutilised. This is often the case with public utility companies operating at national level.
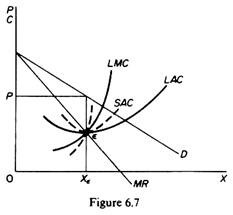
Finally in figure 6.7 we show the case in which the market size is just large enough to permit the monopolist to build the optimal plant and use it at full capacity.
It should be clear that which of the above situations will emerge in any particular case depends on the size of the market (given the technology of the monopolist). There is no certainty that in the long run the monopolist will reach the optimal scale, as is the case in a purely competitive market. In monopoly there are no market forces similar to those in pure competition which lead the firms to operate at optimum plant size (and utilize it at its full capacity) in the long run.