Effects of Lump-Sum Taxes in a Competitive Industry

We shall try to know here the effects of the tax on a constant cost competitive industry in the short run and in the long run.

The Short-Run Effects of the Tax:

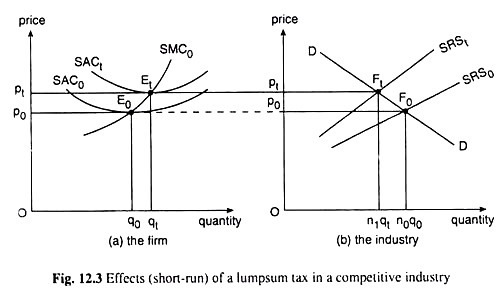
Let us suppose that the picture of a typical firm is given in part (a) of Fig. 12.3 and that of the industry is given in part (b) of the figure. In part (b), the demand curve for the good has been given to be DD. On the other hand, the supply curve of the industry before the imposition of the tax has been given to be SRS₀ which is the horizontal summation of the SMC curves of the individual firms in the industry.

The number of such firms is, say, n₀. Initially, i.e., before the imposition of the tax, the demand-supply equilibrium price, p₀, of the good has been determined at the point of intersection F₀ of the demand (DD) and supply (SRS₀) curves.

We have assumed that at p = p₀, the firm is in short-run and long-run equilibrium at the minimum point of its average cost curves (the long-run AC curve has not been shown), producing q = q₀. Therefore, at p = p₀, the industry output has been n₀qo at the point F₀.

To obtain the effects of a lump-sum tax, let us now suppose that the government imposes such a tax of a lump-sum amount of T (Rs) per period, on the good. The firm that produces the good will take it as an increase in its total fixed cost (TFC) per period, and as TFC increases by T, the firm’s total cost (TC) would also increase by T at each output.

The firm’s short-run average cost (SAC) also increases by T/q at any output q, and so its SAC curve will shift upwards from SAC₀ to SAC_t.

The vertical gap between the SAC_t and SAC₀ curves at any output q is equal to T/q, and, for obvious reasons, it falls as q increases. Since the imposition of the lump-sum tax keeps the firm’s total variable cost (TVC) function unaffected, it keeps the firm’s MC function also unaffected, i.e., the firm’s MC function would remain the same as it was before the imposition of the tax—it would remain the same SMC₀, and so, the SRS₀ curve of the industry which is the horizontal summation of the SMC curves will also remain the same after the imposition of the tax, given the number of firms.

As we know, the SMC curve crosses the SAC function at the latter’s minimum point. Therefore, the SMC₀ curve would cross the SAC₀ and SAC, curves at their minimum points, E₀ and E_t. Since the SMC curve at E₀ is positively sloped, the point E_t would lie upward towards right of point E₀, i.e., the firm’s output q_t at E_t, would be larger than the output q₀ at the point E₀.

Since the SRS curve of the industry, viz., SRS₀, does not change its position as a result of the imposition of the tax, the price of the good would remain the same at p = p₀, and since the SMC curve of the firm would not change its position, the output of the firm, q₀ would remain the same, and the number of firms remaining the same at n₀, the industry output would also remain unchanged at n₀q₀.

But now the SAC curve of the firm has shifted upwards from SAC₀ to SAC_t. Therefore, at the p = MC point E₀ (p₀, q₀), the firm would have p < SAC, i.e., the firm would earn economic losses in the short run as a result of the imposition of the lump-sum tax.

The Long-Run Effects of the Tax:

In the long-run adjustment process, some of the firms would be leaving the industry to avoid economic losses. Therefore, the SRS curve of the industry being a horizontal summation now of a smaller number of SMC curves, would be shifting to the left of SRS₀.

The DD curve remaining in the same position, the price of the good now would be rising from p₀. The process would continue till the number of firms diminishes to, say, n₁ (n₁ < n₀), and the SRS curve shifts to the position of SRS_t that intersects the DD curve at F_t to give us p = p_t which is a price that puts the firm again in the normal profit-earning equilibrium, for, at p = p_t, and at the point E_t, the firm’s AR = MR curve touches the SAC_t curve and intersects the SMC curve.

At p = p_t, the firm’s output would be q = q_t which would be larger than q₀, and the industry output (at the point F_t) would be n₁q₁, which is less than the initial level of n₀q₀. This is because the number of firms in the industry has decreased although the output of each firm has increased.

We may summarise the short-run and long-run effects of the tax in the following table: