Inefficiency of Monopoly | Markets

Each firm in a competitive industry operates at a point where its MC becomes equal to the (exogenously given) price of the product. That is why the short-run supply curve of a competi­tive industry is the horizontal summation of the short-run supply curves (or the short-run MC curves on and above the minimum AVC) of individual firms.

Therefore, a competitive industry operates at a point where price equals marginal cost. A monopolized industry, on the other hand, operates where price is greater than MC. Thus, in general, price will be higher and output lower under monopoly than under competition.

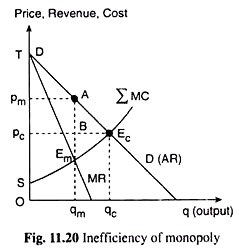
We may illustrate the point with the help of Fig, 11.20. In this figure, DD is the demand curve for the product of a competitive industry, and EMC is the industry’s supply curve. Therefore, the market (demand = supply) equilibrium point will be E_c, which is the point of intersection between the DD and the IMC curves.

At this point, the price of the product will be p_c = op_c and the quantity demanded and supplied will be q_c = oq_c. All the firms would operate at their respective p = MC points. Let us now assume that the competitive industry with all its firms becomes monopolized under a single owner, i.e., the competitive industry now becomes a multi-plant monopoly.

The demand curve DD for the product now becomes the AR curve of the monopolist and its corre­sponding marginal curve is given by MR in Fig. 11.20.

Now, in order to minimise the cost of production of any particular quantity of output, the monopolist would have to distribute the production of that quantity over the different plants in such a way that MC in each plant may become the same, and this MC would be the MC of that particular quantity of output.

Understood in this way, the MC of any particular quan­tity of output produced by the multi-plant monopolist would be given by the curve EMC of Fig. 11.20, which is the horizontal summation of the MC curves of indi­vidual plants.

The profit-maximising equilibrium point of the monopolist in this case would be the point of intersection (E_m) between the MR and the ∑MC curves. At this point, the output of the monopolist would be q_m = Oq_m which would be less than the competitive output q_c = Oq_c and the price charged by the monopolist would be p_m = Op_m which is greater than MC (= E_m q_m) and which is greater than the competitive price (p_c).

Since the price under monopoly is greater and output lower than under competition, the consumers would always be worse off in a monopolistic industry than in one under perfect competition. But a portion of the consumers’ loss would be converted into the gain of the industry.

This can be seen in Fig. 11.20. Here, as we move from competition to monopoly, i.e., as the equilibrium (p, q) combination moves from (p_c, q_c) to (p_m, q_m), the consumers’ surplus diminishes by □p_cp_mAE_c (from □TpcE,. to □Tp_mA) and of this, □p_cp_mAB is converted into the producer’s surplus under monopoly.

Producer’s surplus, □Sp_cE_c, decreases by □BE_mE_c and increases by □p_cp_mAB. Taking both the industry’s gain and the consumers’ loss into con­sideration, it is not clear which would be the better arrangement for the society—competition or monopoly, unless we make a value judgement about the relative welfare of the consumers and of the owners of the industry.

However, we may argue against monopoly on grounds of efficiency alone. An economic arrangement is Pareto-efficient if there is no way to make anyone better off without making somebody else worse off. We shall now see that the level of output under monopoly is not Pareto-efficient.

Let us remember that at any point on the demand curve of a monopoly firm like DD in Fig. 11.20, the price p stands for how much people are willing to pay for the marginal unit of the good.

Since p is greater than MC for all output levels between q_m and q_c, there is a whole range of output (i.e., between q_m and q_c) where people are willing to pay more for the marginal unit of output than it costs to produce it. Clearly, there is a case for a Pareto improvement here.

For example, let us consider the situation at the monopoly level of output q_m. Since p(q_m) > MC (q_m), we know that there is someone who is willing to pay more for an extra unit of output than it costs to produce that extra unit. Let us suppose that the firm produces an extra unit and sells it to this person at any price p where p(q_m) > p > MC(q_m).

Then this consumer is made better off because he was just willing to pay p(q_m) for that unit of consumption, and it was sold for p < p (qm). Similarly, it cost the monopolist MC(q_m) to produce that extra unit of output and he sold it for p > MC(q_m).

If all the other units of output are being sold for the same price as before, then from the sale of the extra unit, both sides of the market—the buyers’ side and the sellers’ side— are better off and no one else is made worse off. Therefore, we have found here a Pareto improvement. That is, the usual monopoly solution (p_m, q_m) is Pareto-ineflicient.

The reason for this inefficiency of monopoly is this. In the case of competition, price is constant irrespective of output, making MR at any output a constant and equal top. So the firm’s profit maximising p = MR = MC point is also the Pareto-efficient p = MC point.

On the other hand, since the AR curve of the monopolist is downward sloping, the extra revenue (MR) obtained from selling the marginal unit of output is not equal to, but less than, the price of that unit (i.e., MR < p). That is why, in monopoly, the firm’s profit maximising MR = MC point is a Pareto-inefficient p > MC point.