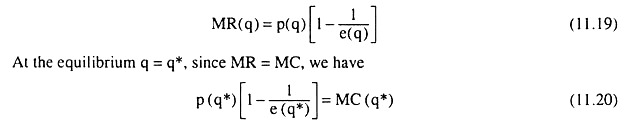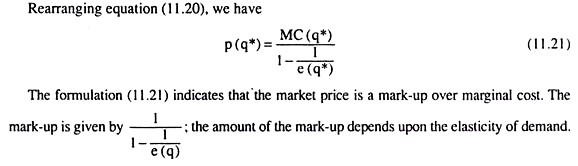We can use the elasticity formula given below for the monopolist to express its optimal pricing policy.
This formula is:
Since the monopolist always operates where the demand is relatively elastic, we are assured that e > 1, and thus the mark-up is greater than 1. We also observe that larger the value of e, the smaller would be mark-up over the MC, which is what is expected, for the larger the price- elasticity of demand, the smaller would be the option before the monopolist to charge a higher price.
ADVERTISEMENTS:
In the case of a constant-elasticity demand curve, formula (11.21) is especially simple. Since e = constant, the mark-up here would also be a constant. For example, if e = 3 = constant, the mark-up would be 1.5 = constant.
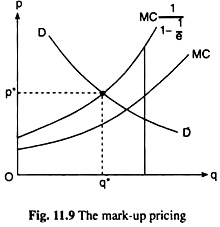
Therefore, a monopolist who faces a constant elasticity of demand will charge a price that is a constant mark-up (which is 1.5 when e = 3) on MC. This is illustrated in Fig. 11.9. Here the curve labeled MC[1(1-1/e)] is constant fraction higher (1.5 times higher) than the MC curve.
In Fig. 11.9, let us suppose, the demand curve of the monopolist with constant elasticity, e = 3, is DD, the marginal cost curve is MC and the curve labeled C is constant fraction (1.5 times) higher than the MC curve. The MC[1(1-1/e)] curve shows us what price the profit-maximising monopolist would like to charge with a mark-up on MC at any particular equilibrium output.
ADVERTISEMENTS:
Now, if the equilibrium MR =MC output is q*, then the equilibrium price at that output with the stipulated mark-up on MC would be p*. Therefore, here, the equilibrium price-quantity combination of the monopolist is obtained to be (p*, q*) which must lie also on his demand curve. In other words, (p*, q*) must be the point of intersection of the demand curve, DD, and the MC[1(1-1/e)] curve.
In our above discussion, we have seen therefore how the elasticity formula (11.19) can be used to express the pricing policy of the monopolist in an alternative way.