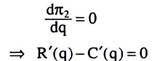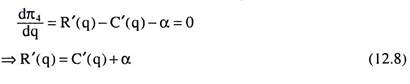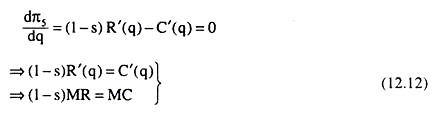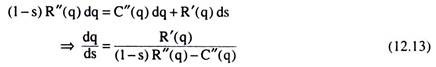Study of Lump-Sum, Profit and Sales Tax in Monopoly

The below mentioned article provides a comparative study of lump-sum tax, profit and sales tax in monopoly.

In the case of a monopoly, a lump-sum or a profit tax is better than a sales tax. This is because a lump-sum tax, or a profit-tax with a marginal rate less than 100 per cent, will reduce the profit after taxes of a (profit-maximising) monopolist, but will not affect his optimum price-quantity combination.

On the other hand, a sales tax, whether based upon quantity sold or upon value of sales, will reduce his profit and output levels and increase his price. We may prove this in the following way. The monopolist cannot avoid a lump-sum tax. It must be paid regardless of the physical quantity or value of his sales or the amount of his profit. Before the imposition of the tax his profit (π₁) is

π₁ = R(q) – C(q)                                (12.1)

where R (q) and C(q) are his total revenue and total cost which are functions of his output quantity, q. But after the imposition of the tax, his profit becomes

π₂ = R(q) – C(q) – T                         (12.2)

where T is the amount of the lump-sum tax.

The first order condition (FOC) for profit maximization before the imposition the tax, is

Also, the FOC for profit maximization after the tax is imposed, is

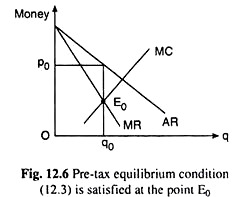
From (12.3) and (12.4) it is evident that the monopolist’s price-output combination is determined at the point of equality between MR and MC, both before and after the imposition of the lumpsum tax.

Also, the second order conditions (SOCs) for profit maximization, both before and after the tax, i.e., (d²π₁)/dq2 < 0 and (d²π₂)/dq2 < 0 are identical, both of them giving us:

R” (q) – C”(q) < 0. It is obvious from the shapes of the MR and MC functions in Fig.12.6 that the SOC is satisfied at both the pre-tax and post-tax equilibrium points.

Since the AR,MR and MC functions are not affected by the lump-sum tax, his price-output combination is also not affected by the imposition of the tax.

Let us now come to the profit tax. A profit tax requires that the monopolist pays the government a specified proportion of the difference between his total revenue and total cost. If the tax is a flat rate constant proportion, his profit after tax payment is

Where 0 < t < 1 is the rate of profit-tax

Now, the FOC for profit maximization after the imposition of the profit tax is

Since 1 – t ≠ 0, we have

It is evident from (12.3) and (12.6), and also from identical SOCs [i.e., R”(q) – C”(q) < 0], that the monopolist’s price-output combination remains unaffected by the imposition of the profit tax.

Lastly, let us consider a specific sales tax of Rs α per unit of output.In this case, the post-tax profit function of the monopolist would be

The first order condition (FOC) for profit maximization after the imposition of the tax is

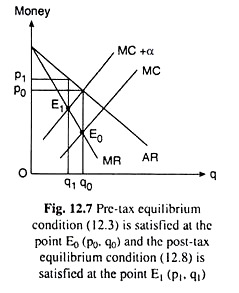
We obtain from (12.8) that the monopolist maximises his profit after the imposition of sales tax by equating MR with MC plus the sales tax per unit. Equations (12.3) and (12.8) give us that the price-output combination of the monopolist before and after the imposition of sales tax per unit would not be the same.

This is because the (MC + a) function would lie above the original MC function at a vertical distance of a (= constant).

And in this case, the MR function would intersect the (MC + a) function at a smaller output. Therefore, after the tax, the output of the monopolist would be smaller and given the negative slope of the AR (q) function, price would be higher (Fig. 12.7). We may also obtain this point mathematically in the following way.

Since R”(q)-C”(q) is less than zero by the second order condition (SOC) of profit maximisation, viz., d²π₄/dq² < 0, we have

dq/dα < 0

i.e., the optimum output level declines as the rate of sales tax increases. In other words, the imposition of a specific sales tax (per unit) results in a smaller quantity sold, and, as the quantity sold becomes smaller, price of the product becomes higher (given the negative slope of the AR function).

The results are similar, if the sales tax is a proportion of the value of sales (total revenue). In this case, the profit function of the monopolist after the imposition of the tax would be

π₅ = R(q)-C(q) – sR(q)

= (1-s) R(q) – C(q)                                (12.11)

where 0 < s < 1 is the rate of sales tax.

The first order condition for profit maximisation is

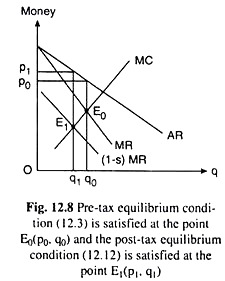
Eqn. (12.12) gives us that profits are maximised by equating MC to the portion of MR that the monopolist is allowed to retain after the payment of the tax. Obviously this condition is different from (12.3).

In the present case, the function on the LHS of (12.12) would lie below the original MR function, and it would intersect the MC function at a smaller output and higher price (given the negative slope of the AR function) (Fig. 12.8). Mathematically, we obtain the following.

Taking the total differential of (12.12):

Since the first order condition (12.12) for π-max requires that R'(q), or, MR > 0 [as MC is assumed to be positive] and the second order condition, i.e.,d²π₅/dq² < 0 implies that the denominator of (12.13) is negative, we have, dq/ds < 0.

In other words, the imposition of an ad valorem sales tax also results in reduced output and increased price. On the basis of the above analysis we may conclude that in the case of monopoly, a lump-sum tax or a profit-tax is better than a sales tax, whether based on the quantity sold or on value of sales.