An important application of indifference curves is to explain the mutual exchange between two individuals of two goods possessed by each.
When the two individuals have to exchange two things, the case is one of bilateral monopoly.
It should be noted that inventor of indifference curves, Y. F. Edgeworth applied them to explain exchange of goods between two individuals. Suppose there are two individuals, A and B. Both individuals and B have some amount of goods X and Y. They are to exchange these goods between themselves.
Now, with the help of indifference curves it can be proved that the exchange of two goods between the two individuals will be of mutual advantage to both of them, that is, the exchange of goods between the two individuals will add to their combined welfare. This can be illustrated with the help of Figures 11.1 and 11.2. In Figure 11.1, indifference map depicting the scale of preferences of individual A between the two goods X and Y is drawn.
Likewise in Figure 11.2 indifference-map of individual B depicting his scale of preferences between the two goods X and Vis drawn. Now, the exchange problem between the two individuals and its resultant welfare implications can be analysed with the help of Edgeworth Box diagram which has been named after its inventor Y. F. Edgeworth who first of all discussed this exchange problem.
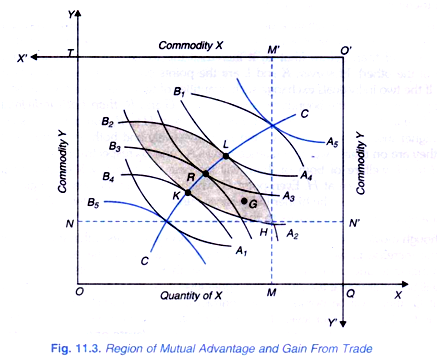
In order to make the Edgeworth Box diagram, we have to turn upside down (that is, turning around 180°) the indifference map of one individual. So in Figure 11.3, we have turned around 180° the indifference map of individual B with O ‘ as the origin. Suppose individual has OM quantity of X and ON quantity of Y. The individual B has O ‘M’ of good X and O ‘N’ of good Y. Thus OQ and OT are the dimensions of the rectangular Edgeworth Box. A1, A2, A3, A4, etc. are the successive indifference curves between two goods of individual A, and B1, B2, B3, and B4 are the successive indifference curves between the two goods of individual B.
Thus, in the Edgeworth Box diagram, the indifference maps of two individuals are combined by turning the indifference map of one individual upside down. There are several points at which the indifference curves of two individuals are tangent to each other.
ADVERTISEMENTS:
If all these tangency points between the two sets of indifference curves are joined together we get a curve CC which is called the Contract Curve. It is at any point on this contract curve that the exchange or trade of goods between the two individuals will take place. Further, it will be to the mutual advantage of the individuals to move from a point away from the contract curve to a point on the contract curve. This will be understood from me following analysis.
Since the initial distribution of two goods is that individual A has OM of good X and ON of good Y and individual B has O’ M’ of X and O’N’ of Y, the two will be at point H in the Edgeworth Box. Now, every point within or on the boundaries of the shaded area represents a possible act of exchange to the mutual advantage of both individuals because it leaves them either at their initial indifference curves A3 or B3, respectively as the case may be and possibly on the higher indifference curves of both of them.
Therefore, the shaded region has been called the region of mutual advantage. With initially at point H on which the individuals A and B are respectively at their indifference curves A2 and B2 if the two individuals move to the point K after exchanging some quantities of the two goods, then the individual A has been put on higher indifference curve A4 and individual B remains at same indifference curve B2.
ADVERTISEMENTS:
Thus, with the contemplated exchange, individual A has been made better off than before (his welfare or satisfaction has increased), while individual B is no worse off than before welfare or satisfaction remains the same). Likewise, if the two individuals move to the point K after exchanging some quantities of the goods, individual B has been put on a higher indifference curve B4 and therefore he has become better off than before, whereas individual A remains at A2 and therefore no worse off than before.
It is thus clear that exchange of goods between the two individuals involved in moving from point H to either L or K is to their advantage; it makes one better off without making other worse off than before (that is, it increases the welfare of one without reducing the welfare of the other). However, K and L are the points on the boundary lines of the shaded region. If the two individuals exchange such quantities of two goods that they move from point H to any point within the boundaries such as point G and R, then both then both individuals will be better off than before.
For instance, if they move from H to R, both individuals A and B are put at higher indifference curves A3 and B3 respectively and both are better off than at H where they are on their lower indifference curves A2 and B2 respectively. Similarly, in moving from H to G, welfare of both of them will increase since they will be put on the higher indifference curves than at H. Even point G, which lies within the shaded region but off the contract curve, will be on the higher indifference curves of the two individuals than H, because the indifference curves are convex to the origin.
Though moving from point H to a point such as G which lies within the boundaries would mean the increase in welfare of both individuals, but it will not be equilibrium point, since corresponding to any point off the contract curve, there will be points on the contract curve which will be better than it (i.e., will mean higher level of welfare for both).
Thus corresponding to point G there will be points on the contract curve which will lie on higher indifference curves and will mean higher level of welfare for both the individuals than point G In welfare economics, the points on the contract curve are known as Pareto optimum since they indicate the situation of maximum social welfare where no individual can be made better off without making other worse off, and the points off the contract curve are known as Pareto sub-optimum where there is possibility of making all individuals better off or some better off without making others worse off.
Therefore, it follows that the two individuals will voluntarily exchange goods X and Y until they reach a point such as K, R or L on the contract curve where their Indifference curves are tangent to each other. Having reached the contract curve, no further changes of mutual benefit can be made. Thus, in equilibrium, change of goods (that is, trading) between the two individuals will occur at a point on the contract curve within the shaded region relative to the initial point H.
Though when the individual moves from point H to a point on the contract curve between K and L he will be better off than at H, all points on the contract curve are not equally advantageous to both the individuals. As we move from point K towards L on the contract curve, individual A will be going to his higher indifference curves but individual B will be going to his lower indifference curves.
Thus while trading individual A will want to go to the point L, while individual B will try to go to the point K. On the contract curve, where the two individuals will end up in their exchange depends on their respective bargaining strengths which will determine the rate of exchange between the two goods possessed by them.
It follows therefore that the trade or exchange between the two individuals will ultimately take place at any point on the contract curve between K and L. The greater the bargaining strength of individual A, the trading point will be nearer to L. On the other hand, the greater the bargaining strength of individual B, the trading point will be nearer to K. Thus moving along the contract curve means the increase in the satisfaction or welfare of one and reduction in the welfare of the other. That is why contract curve is also known as Conflict Curve.
ADVERTISEMENTS:
For assessing whether the aggregate welfare (that is combined welfare of the two individuals) increases or decreases as we move along the contract curve, we have to make interpersonal comparison of utility which following Pareto most of the economists refuse to do so. Thus, according to economists, so far as movement from a point off the contract curve to the point on the contract curve is concerned, it definitely and unambiguously increases the aggregate welfare of the two individuals.
But the changes in aggregate social welfare cannot be assessed when the contemplated move is from one point of the contract curve to another on it, unless we are willing to make interpersonal comparison of utility. To conclude, “An unwillingness to make interpersonal comparison of utility means that the only changes that can be evaluated are those that make everyone better off or that makes at least one person better off without anyone else worse off. An improvement in some people’s welfare at someone else’s expense cannot be judged in quantitative utility terms. A movement toward the contract curve always represents an unambiguous improvement of aggregate welfare but a movement along the contract curve alters the distribution of aggregate welfare among the participants in the market.”
It is now clear from above that with the help of indifference curves why the exchange or trade between the two individuals will take place and what gain from this exchange or trading of goods they will obtain in terms of increment in their welfare can be ascertained. Further, indifference curve analysis clearly brings out that it is to the advantage of both individuals to exchange goods between themselves.