The following points will highlight the top three marginal conditions for Pareto optimality. The marginal conditions are: 1. Pareto Optimality for Exchange 2. Pareto Optimality for Production 3. Pareto Optimality for Exchange and Production.
Marginal Condition # 1. Pareto Optimality for Exchange:
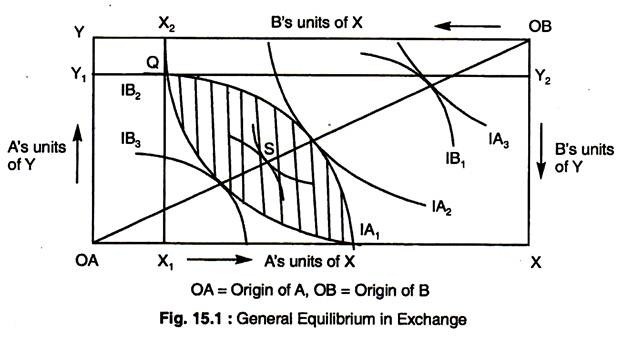
We know that general equilibrium in exchange is achieved on the contract curve of the Edge-worth Box diagram.
A point on the contract curve also represents Pareto optimality for exchange (see Fig. 15.1) because once the contract curve is reached, no further exchange can improve the welfare of one without reducing the welfare of another. If no more exchange can occur without harming someone, then Pareto optimality has been attained.
We now move from a two-individual economy to one composed of many consumers, and also show that Pareto optimality for exchange is satisfied under conditions of perfect competition.
ADVERTISEMENTS:
We know that the contract curve represents all the tangency points of the two individuals’ indifference curves; thus, at all tangency points, the slopes of the indifference curves are the same, and, hence, the two individuals have the same MRS. We know that each individual will maximise his satisfaction by equating his MRS for any two goods to the ratio of their prices.
Since the price of each good is the same for every consumer in a perfectly competitive economy, the ratio of the prices of any two goods is the same for all consumers. Therefore, every consumer will maximise his satisfaction by equating MRS for any two goods to the same price ratio.
This is true for any number of goods and any number of consumers. Thus, Pareto optimality for exchange is satisfied under perfect competition.
ADVERTISEMENTS:
Marginal Condition # 2. Pareto Optimality for Production:
Pareto optimality for production is attained on the contract curve of the Edge worth Box diagram for production. If the producers are not on the contract curve, it would be possible, through the exchange of inputs for both producers, to reach higher output isoquants.
Once on the contact curve, it would not be possible for either producer to move to a higher isoquant without the other provider moving to a lower one. In addition, the contract curve represents all tangency points of the two producers’ isoquants and, thus, the two producers have the same MRTS at any point on the contract curve.
In a perfectly competitive economy with large number of firms, Pareto optimality for production is achieved by means of the input price mechanism. Each profit-maximising producer will employ two inputs in such a way that the MRTS = the ratio of the input prices. In a perfectly competitive economy, each producer pays the same price for a given input, and, so, the ratio of any input price must be the same for all producers.
ADVERTISEMENTS:
Thus, all producers will equate their MRTS for any two inputs to the-same input price ratio, in which case, all producers will have the same MRTS for any two inputs. Hence Pareto optimality for production is achieved in a perfectly competitive economy where MRTSLK = w/r.
Marginal Condition # 3. Pareto Optimality for Exchange and Production:
The third marginal condition for maximum social welfare requires the MRS for any two goods to be equal to the MRT for those goods. We have already seen that the level of consumer satisfaction could be increased if MRS ≠ MRT. So, a condition for general equilibrium and for Pareto optimality is that the MRS in consumption must equal the MRT in production for any two goods.
We can gain further insight into these marginal conditions by demonstrating how they are satisfied in a perfectly competitive economy. First, in a perfectly competitive economy, the MRT for any two goods will equal the price ratio of these two goods.
To see how it works, let us suppose that the MRT does not equal the price ratio of two goods. Suppose the two goods are X and Y, with price PY = £1 and PY = £1, and the MRT is 1Y: 3X. By transferring one Y into three X, producer loses £1 in Y but gains £3 in X, for a net gain of £2.
Thus, producers will continue to produce more X and less Y until the MRT equals the price ratio of X and E Finally, in a competitive economy, all producers and consumers are confronted by exactly the same price for X and Y, and, hence, the same price ratio for the two goods.
Thus, all MRSs and MRTs are equal to the same price ratio for X and Y. Since the MRSs and MRTs are equal to the same price ratio, they are equal to each other. Therefore, the third marginal condition for Pareto optimality is satisfied by a perfectly competitive economy.