Daniel Bernoulli evinced great interest in the problem known as St. Petersburg paradox and tried to resolve this. St. Petersburg paradox refers to the problem why most people are unwilling to participate in a fair game or bet.
For example, offer of participating in a gamble in which a person has even chance (that is, 50-50 odds) of winning or losing Rs. 1000 is a fair game.
To put in mathematical terms, a gamble whose expected value is zero, or more generally, the game in which the fee for the right to play is equal to its expected value is a fair one. Thus, according to St. Petersburg in an uncertain game a most individuals will not make a fair bet or, in other words, will not play the fair game.
Daniel Bernoulli provided a convincing explanation of the said behaviour of rational individual. According to him, a rational individual will take decisions under risky and uncertain situations on the basis of expected utility rather than expected monetary value.
ADVERTISEMENTS:
He further contended that marginal utility of money to the individual declines as he has more of it. Since the individual behaves on the basis of expected utility from the extra money if he wins a game and the marginal utility of money to him declines as he has extra money, most individuals will not ‘play the game’, that is, will not make a bet. It is in this way that Bernoulli resolved ‘St. Petersburg paradox’.
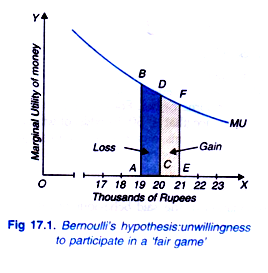
A graphic illustration will make clear Bernoulli’s solution to the paradox. Consider Figure 17.1 in which on the X-axis, the quantity of money (thousands of rupees) and on the Y-axis, marginal utility of money (rupees) to an individual are measured. Suppose an individual has 20 thousands of rupees with him and can make a bet at even odd (i.e., 50-50 chance) of winning or losing rupees one thousand.
If he wins the bet, money with him will rise to 21 thousand (20 + 1) rupees. If as a result of an increase in money with him, his expected marginal utility of money declines, then the expected marginal utility of extra one thousand rupees to him which is depicted by the rectangle CDFE is less than the extra marginal utility of the previous one thousand (i.e., 20th thousand) rupees which is measured by the rectangle ABDC.
In other words, the gain in utility in case of his winning the bet is less than the loss of utility in case of his losing the bet, though the gain and loss is the same in terms of monetary amount (i.e., Rs. one thousand). Thus, given the diminishing marginal utility of money the expected gain in utility is less than the expected loss of utility from one thousand rupees involved in the bet, a rational individual will therefore not make a bet with 50-50 odds.
It may be further noted that a rational individual would even be unwilling to bet or gamble even at favourable odds if his marginal utility of money declines very rapidly. For example, if a person is offered a bet; if he wins the bet, he will be given Rs. 1500 and if he loses it, he has to pay Rs. 1000, then, as in case of rapid decline in marginal utility of money, he may be unwilling to agree to make the bet. Consider Figure 17.2 where the individual has Rs. 20,000 at present.
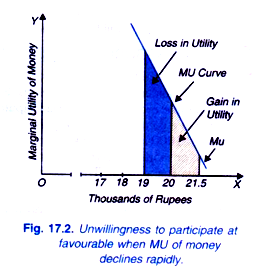
In case he wins the bet, his monetary gain will be Rs. 1500 which will raise his money income to Rs. 21,500 and gain in his total utility will be given by the black-shaded area and if he loses the bet, his income falls by Rs. 1000 to Rs. 19,000 and as a result he suffers a loss in total utility equal to the red-shaded area.
It will be observed from Figure 17.2 that despite a smaller loss in money terms, the loss in terms of total utility is greater than the gain in total utility despite a greater increase in money in case he wins the bet. This happened due to the rapid decline in marginal utility of money as individual’s money increases.
It may be pointed out that in our discussion aboveabout the individual’s betting it is assumed that individual derives no pleasure from gambling, that is, he does not enjoy gambling for its own sake. This is another way of saying that the individual behaves rationally in the sense that he will behave on the basis of expected gains and losses of utility from winning and losing money through gambling.
ADVERTISEMENTS:
Although Bernoulli’s hypothesis that individual decision to participate in a gamble or not, depends on his expected utility rather than expected money value of the game is of crucial significance in any discussion of individual’s behaviour under risky and uncertain situations. So long as there is no upper bound on the utility function, the prize in a gamble can be appropriately adjusted so that the paradox is regenerated. Further Bernoulli’s main point that an individual considers expected utility from the extra money rather than monetary value of the gain itself has found wide acceptance among economists.
However, a major drawback of Bernoulli’s expected utility hypothesis is that it assumes cardinally measurable utility which economists today find it difficult to believe. J. Von Neumann and O. Morgenstern adopted an entirely new approach to assigning numerical values to the utilities obtained from extra money by the individuals behaving in risky or uncertain situations, such as in case of gambling and insurance and they based their method of constructing utility index (which is envied at in a different way from the cardinal measurement of utility by neoclassical economists) on the expected utility hypothesis of Bernoulli. They showed that we can analyse the choice by an individual under risky and uncertain situation on the basis of N – M utility index.
Neumann-Morgenstern Utility Concept Index under Risky Situations:
Making use of Bernoulli’s idea that under risky and uncertain prospects as in betting, gambling and purchasing lottery tickets etc., a rational individual will go by the expected utilities rather than expected money values, Neumann and Morgenstern in their now famous work ” Theory of Games and Economic Behaviour gave a method of numerically measuring expected utility from winning prizes. On the basis of such utility index, called N-M index rational decisions are made by the individuals in case of risky situations.
Thus, Neumann- Morgenstern method seeks to assign a utility number or in other words, construct N-M utility index of the total utility of money which a person gets as his stock of money wealth increases. The choices by an individual under risky and uncertain situations depend on N-M utility index (i.e. expected numerical utilities) and with changes in money income.