Indifference curve analysis can be used to explain underwhat conditions rationing of goods by the Government can act as binding or a constraint on consumer’s choices and further how it affects his welfare.
It may be noted that income of a consumer along with the prices of goods serves as a constraint on his choices and is often called a budget constraint.
This budget constraint can be written as follows:
Px. X + Py. Y < M
ADVERTISEMENTS:
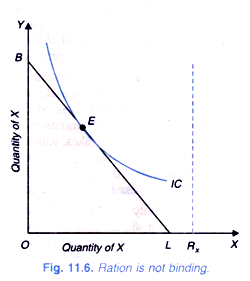
The above inequality implies that consumer can choose a combination of goods from within or on the market opportunity set. With given income of the consumer and prices of the two goods, we draw a budget line BL in Figure 11.6. The shaded region bounded by the budget line BL and the coordinate axes represents market opportunity set from which the consumer can make a choice of the two commodities. If now the Government introduces a rationing for commodity X and fixes a ration of X equal to ORx (At point Rx we have shown a vertical line showing the constraint or ration limit imposed by the rationing fixed at ORx).
It will be seen that with ration limit fixed at ORx, rationing does not act as a binding at all and prove to be quite ineffective in restricting the consumption of good X which is the objective of the policy. Such a situation is relevant in case of a poor family whose income is so small that it cannot buy even the rationed quantity. It is the income that serves as a binding on his consumption choice and not the ration limit.
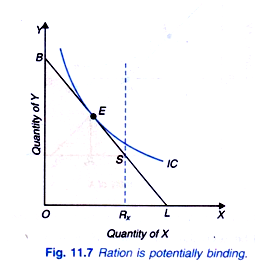
Now consider Figure 11.7 where ration limit is fixed at Rx which lies to the left of L. This ration limit reduces or truncates his market opportunity set (i.e. set of attainable combinations of two goods X and Y) as shown by the reduced shaded area in Figure 11.7 and therefore in this case the ration limit is only potentially binding on him.
ADVERTISEMENTS:
Though the consumer can buy the ration amount, that is, ration limit is attainable but he is not willing to consume good X as much as the ration limit permits him. He is in equilibrium at point E where he consumes quantity of good X which is smaller than the ration amount Rx,. Thus, his preferences are such that rationing is not actually binding for him.
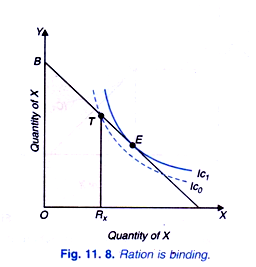
However the more important and relevant case of rationing is depicted in Figure 11.8. In this case, ration limit fixed Rx lies to the left of his equilibrium position E. Without the restriction of rationing he will consume a larger amount of commodity X and is at indifference curve IC1 With the budget line BL and the rationed quantity Rx, he will be at point T which lies at lower indifference curve IC1.
ADVERTISEMENTS:
Thus ration limit serves as a binding for him and forces him to consume less of good X and more of good Y than he prefers. That is why at point T in Fig. 11.8 he is at lower indifference curve IC0 indicating his lower level of welfare. Thus, in this case, rationing is actually binding for the consumer and reduces his welfare.
Rationing of both the Commodities:
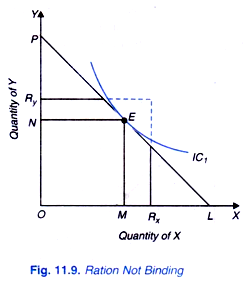
We will now explain the consequences if both the commodities X and Y are rationed. In particular we are interested in knowing whether it is the ration limits or income of the consumer that is binding, that is, which forces the consumer to consume less amounts of the goods. In Figure 11 .9 with a given income and prices of the two goods X and Y the consumer is in equilibrium at E buying OM of commodity X and ON of commodity Y. Now, suppose with the introduction of rationing, ration limit Rx is fixed for good X and RY for good Y.
It will be seen from Figure 11.9 that ration amounts of Rx and Ry of goods X and Y respectively are greater than OM and ON which the consumer is buying with his price-income situation. Therefore, the ration limits in this case are not actually binding since these do not anyway constraint his consumption.
Of course, these ration limits narrow down or truncate his market opportunity set at both ends on the X and Y axes, and in this way they are potentially binding but they are not effective in restraining his consumption. Therefore, this can be interpreted to be the case of a poor family whose optimum consumption basket of the two goods is small because of low income and therefore remains unaffected if ration limits are set at higher levels.
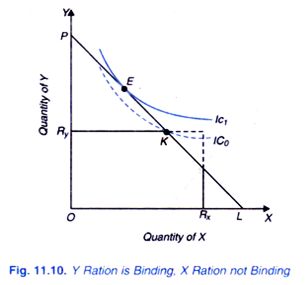
Now, consider Figure 11.10 where it will be seen that ration limit Ry is smaller than consumer’s optimum consumption of Y as indicated by combination E of the two goods on the budget line PL which has been drawn with his given income and prices of two goods. But ration limit Rx for good X is larger than his optimum or equilibrium consumption quantity of good X. It follows therefore that for good Y ration limit is actually binding as it forces the consumer to point K on a lower’ indifference curve IC0 than optimum point E on indifference curve IC1, at which he would have been without the restriction of rationing.
On the other hand, in case of good X in Figure 11.10 the ration limit does not seem to be effective, though it is potentially binding as it truncates his market quantity set. It will be observed that binding by rationing lowers his level of welfare as he is forced to come to the point K on a lower indifference IC0 where he consumes less of good Y than he prefers.
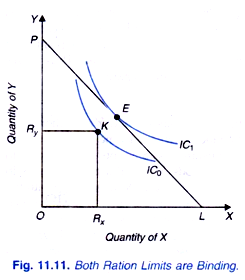
In Figure 11.11. both ration limits Rx and Ry are actually binding and force the individual to consume less of both the commodities than he consumes at his equilibrium position E in the absence of rationing of the two commodities. Figure 11.11 depicts the case of rich people who without the binding of rationing is at point E on indifference curve IC1 and is consuming greater quantity of the two goods than the ration amounts. Introduction of rationing limits forces him to come to point K on lower indifference curve IC0 and consume less amounts of both the goods than he would do without the restriction of rationing. Thus in this case rationing is actually binding on him and reduces his welfare.