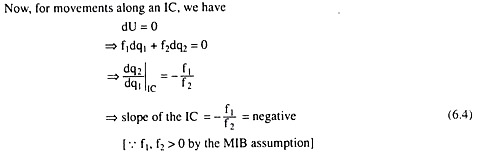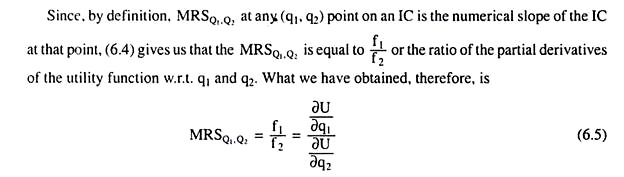Concept of Marginal Rate of Substitution (With Equations)

In this article we will discuss about the concept of marginal rate of substitution, explained with the help of suitable diagram and examples.

The Marginal Rate of Substitution (MRS):

Before establishing the four properties of ICs, first elaborate the idea of MRS. Marginal rate of substitution of good X for good Y (MRS_X, y) at any point in the commodity space, is defined to be the quantity of good Y that the consumer is willing to forego for getting an additional (or the marginal) unit of good X, his level of utility remaining the same.

For example, if the consumer’s level of utility remains unaffected when at any point in the commodity space, he foregoes 3 units of good Y for getting an additional unit of good X, then his MRS_{X Y} would be equal to 3 at the said point.

It is very important to note here that MRS is defined at some point in the commodity space. Since any point in this space is also a point on some IC, it may be said that MRS is defined at a point on an IC.

Geometrical Interpretation of MRS_X,_Y:

From the definition of MRS_{X Y}, it is clear that the substitution between the goods takes place provided the consumer’s level of utility remains unaffected, i.e., here as a result of substitution between the goods, the consumer is moving from one point in the commodity space to another, along one of his ICs.

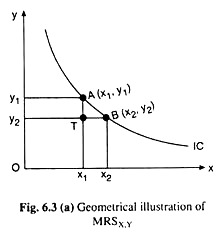
Suppose now that in Fig. 6.3(a), the consumer moves from point A(x₁, y₁) to a very close point B(x₂, y₂) along any one of his ICs, and hence substitutes x₂ – x₁ of good X for y₁ – y₂ of good Y. Therefore, by definition, MRS_X,Y at the point A on the IC would be

Therefore, MRS at any point on an IC is the numerical slope of the IC at that point can be obtained.

The MRS in Mathematical Terms:

Suppose that the utility function of the consumer is given by (6.1). Then the MRS of the good Q) for the good Q₂ may be obtained in mathematical terms in the following way.

The total differential of the utility function (6.1) is:

dU = f₁dq₁ + f₂dq₂ …..(6.3)

where f₁ and f₂ are the partial derivatives, or, the rates of change of U w.r.t. q₁ and q₂, respectively, q₂ and q₁ remaining constant. (6.3) gives the total change in utility, (dU), is (approximately) equal to change in q₁ i.e., dq₁, multiplied by f₁plus the change in q₂, i.e., dq₂, multiplied by f₂.

 

 

 

 

 

 

 

 

 

 

 

 

 

Here remember that in the cardinal analysis f₁ and f₂ are defined as the marginal utilities of the goods Q₁ and Q₂. While it may retain this definition in the present ordinal analysis, do not forget that the partial derivative of an ordinal utility function cannot have any cardinal significance although its sign has an ordinal meaning.

Therefore, the numerical magnitude of the marginal utility of an individual good does not have any meaning here. However, the sign and the ratio of marginal utilities of two goods are meaningful in an ordinal analysis.

For example, a positive value for f₁ indicates that as q₁ increases, the consumer’s satisfaction level also increases, i.e., Q₁ is an MIB good, and he moves to a higher IC. Similarly, the ratio of the MUs is also important, because it would give us the MRS_Q1,_Q2 .

For example, if MU₁ or f₁ = 15 and MU₂ or f₂ = 5 is obtained at any particular point on an IC, i.e., if the ratio of the MUs is obtained to be 3 : 1, then the margin 1 unit of Q₁ would give the consumer the same level of satisfaction as 3 units of Q₂, i.e., the consumer would be willing to forego 3 units of Q₂ for having the marginal unit of Q₁ In other words, the MRS_Q| q₂ in this case is 3 : 1 or 3.