Marginal Rate of Substitution: Principle, Reasons and Relationship between MRS and Marginal Utilities

The concept of marginal rate of substitution is an important tool of indifference curve analysis of demand.

The rate at which the consumer is prepared to exchange goods X and Y is known as marginal rate of substitution.

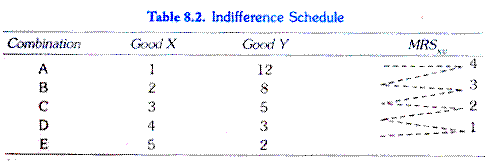
In our indifference schedule I above, which is reproduced in Table 8.2, in the beginning the consumer gives up 4 units of Y for the gain of one additional unit of X and in this process his level of satisfaction remains the same.

It follows that one unit gain in X fully compensates him for the loss of 4 units of it means that at this stage he is prepared to exchange 4 units of Y for one unit of X Therefore, at this stage consumer s marginal rate of substitution of X for Y is 4.

Thus, we may define the marginal rate of substation of X for Y as the amount of Y whose loss can just compensate the consumer for one unit gain in X. In other words, marginal rate of substitution of X for Y represents the amount of Y which the consumer has to give up for the gain of one additional unit of X so that his level of satisfaction remains the same.

In Table 8.2 when the consumer moves from combination B to combination C on his indifference schedule he forgoes 3 units of Y for additional one unit gain in X Hence the marginal rate of substitution of X for Y is 3. Likewise, when the consumer moves from C to D and then from D to E in his indifference schedule, the marginal rate of substitution of X for Y is 2 and 1 respectively.

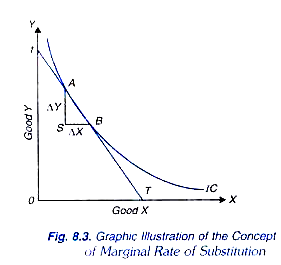
How to measure marginal rate of substitution on an indifference curve? Consider Fig. 8.3 where an indifference curve is shown. When the consumer moves from point A to B on this indifference curve he gives up AS of Y and takes up SB of X and remains on the same indifference curve (or, in other words, at the same level of satisfaction).

It means that the loss of satisfaction caused by giving up AS of Y equals the gain in satisfaction due to the increase in good X by SB. It follows that the consumer is prepared to exchange AS of Y for SB increase in X In other words, marginal rate of substitution of X for Y (MRS_xy) is equal to AS/SB .Now, a small change in the amount of Y such as AS, along an indifference curve can be written as ∆Y and the change in the amount of X as ∆X. Thus, ∆Y shows the amount of Y which the consumer has to give up for the ∆X increase in X if he is to remain on the same indifference curve.

Therefore, it follows that:

Marginal rate of substitution of X for Y (MRS_xy) = AS/SB = ∆Y/ ∆X

Now, suppose that points A and B are very close to each other so that it can be assumed that both of them lie on the same tangent tT (Fig. 8.3). Now, in a right-angled triangle ASB, AS/SB is equal to the tangent of the angle ABS.

It therefore follows that:

MRS_xy = AS/SB = ∆Y/∆X = tangent of <ABS

But in Fig. 8.3 <ABS = <tTO

Hence MRS_xy = tangent of <tTO

But the tangent of <tTO is equal to Ot/OT

Thus tangent of <tTO indicates the slope of the tangent line tT drawn at point A or B on the indifference curve. In other words, the slope of the indifference curve at point of A or B is equal to the tangent of <tTO.

It therefore follows:

MRS_xy = tangent of <tTO = slope of the indifference curve on A or B = Ot/OT

It is thus clear from above that if we have to find out the MRS at a point on the indifference curve we can do so by drawing a tangent at the point on the indifference curve and then measuring the slope by estimating the value of the tangent of the angle which the tangent line makes with the X-axis.

Principle of Diminishing Marginal Rate of Substitution:

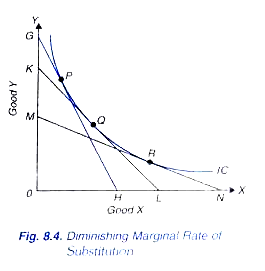
An important principle of economic theory is that marginal rate of substitution of X for y diminishes as more and more of good X is substituted for good K In other words as the consumer has more and more of good X he is prepared to forego less and less of good Y The principle of diminishing marginal rate of substitution is illustrated in Fig. 8.4.

That marginal rate of substitution falls is also evident from the Table 8.2 In the beginning the marginal rate of substitution of X for Y is 4 and as more and more of X is obtained and less and less of Y is left, the MRS_xy keeps on falling. Between B and C it is 3; between C and D it is 2; any finally between D and E, it is 1.

It means from Table 8.2 that as the consumer’s stock of X increases and his stock of Y decreases, he is willing to forego less and less of Y for a given increment in X. In other words, marginal rate of substitution of X for Y falls as the consumer has more of X and less of Y. That the marginal rate of substitution of X for Y diminishes can also be known from drawing tangents at different points on an indifference curve.

As explained above marginal rate of substitution at a point on the indifference curve is equal to the slope of the indifference curve at that point and can therefore be found out by measuring the slope of tangent drawn at a point. In Fig. 8.4 three tangents GH, KL and MN are drawn at the points P, Q and R respectively to the given indifference curve. Slope of the tangent GH is equal to OG/OH.

Hence, marginal rate of substitution of X for Y at point P is equal to Likewise, marginal rate of substitution at point Q is equal to OK/OL and at point R it is equal to OM/ON. It will be noticed that OK/OL is smaller than OG/OH and OM/ON is smaller than OK/OL. It follows that MRS_xy diminishes as the consumer slides down on his indifference curve.

Reasons for Diminishing MRS_xy:

Now, the question is what accounts for the diminishing marginal rate of substitution In other words, why is it that the consumer is willing to give up less and less of Y for a given increment in X as he slides down on the curve? The following three factors are responsible for diminishing marginal rate of substitution.

First, they want for a particular good is satiable so that as the consumer has more and more of a good the intensity of his want for that good goes on declining. It is because of this fall in the intensity of want for a good, say X, that when its stock increases with the consumer he is prepared to forego less and less of good Y for every increment in X. In the beginning when the consumer’s stock of good Y is relatively large and his stock of good X is relatively small consumer s marginal significance for good Y is low, while his marginal significance for good X is high.

Owing to higher marginal significance of good X and lower marginal significance of good Yin the beginning the consumer will be willing to give up a larger amount of Y for one unit increase in good X But as the stock of good X increases and intensity of desire for it falls his marginal significance of good X will diminish and, on the other hand, as the stock of good Y decreases and the intensity of his desire for it increases, his marginal significance for good Y will go up. As a result, therefore, as the individual substitutes more and more of X for Y he is prepared to give up less and less of Y for one unit increase in X.

The second reason for the decline in marginal rate of substitution is that the goods are imperfect substitutes of each other. If two goods are perfect substitutes of each other, then they are to be regarded as one and the same good, and therefore increase in the quantity of one and decrease in the quantity of the other would not make any difference in the marginal significance of the goods. Thus, in case of perfect substitutability of goods, the increase and decrease will be virtually in the same good which cancel out each other and therefore the marginal rate of substitution remains the same and does not decline.

Relationship between MRS and Marginal Utilities:

It can be shown mathematically that MRS_xy between goods is equal to the ratio of marginal utilities of goods X and Y.

An indifference curve can be represented by

U(x ,y) = a …

Where a represents a constant utility along an indifference curve. Taking total differential of (i) above, we have: