Concept of Convex Preference (With Diagram)

In this article we will discuss about the concept of convex preference with the help of diagram.

One of the axioms that define the features of well-behaved indifference curves (ICs) is that averages are preferred to extremes. This is, in short, the concept of convex preference.

That is, take two combinations of goods X and Y, viz., (x₁, y₁ and (x₂, y₂), on the same IC, and take a weighted average such as [(ax₁ + bx₂)/(a +b), (ay₁ + by₁)/(a + b)] of the two combinations where the sum of the weights a and b is equal to 1, then the average combination will be at least as good as, or, strictly preferred to, each of the extreme bundles.

This average combination lies between the two extreme combinations on the straight line connecting them.

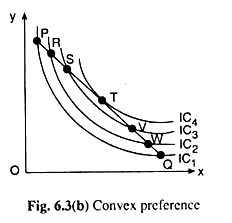
Suppose, in Fig. 6.3(b), P and Q are any two combinations on an IC, P containing a little of X and too much of Y and Q containing too much of X and a little of Y. Also suppose, R is a weighted average of the two extreme combinations, viz., P and Q, and so, R lies between P and Q on the straight line connecting them.

It has been said that R, the average combination, would be weakly or strictly preferred to the extreme combinations, P and Q — in the former case, P, R and Q would be on the same IC, i.e., the IC would have a flat segment, and in the latter case, R would be on a higher IC (here IC₂) than P and Q.

Now suppose that S is a weighted average of the combinations R and Q. Now, if S is strictly preferred to R and Q, it would lie on a higher IC (here IC₃) than the latter two points.

Proceeding this way, come to the combination T which is a weighted average of the combinations S and Q. If T is strictly preferred to the combinations S and Q, then it would lie on a higher IC (IC₄) than the latter two. Suppose that T is the most balanced of the average combinations for the consumer, i.e., it contains the goods in the optimum proportion.

Then if the consumer moves along the straight line PQ or TQ, from T to another combination V which is a weighted average of T and Q, then this combination would become somewhat extreme (that is, with a lesser balance) as compared with T and so it would lie on a lower IC than T, although it would lie on a higher IC than Q for it would be still a preferable average to Q (since it would have a better balance than Q).

It is obtained from the analysis that the concept of convex preference implies that if P and Q are two indifferent combinations, then if the consumer moves along the straight line PQ from the point P towards the point Q, then the points on the way like R, S and T would lie on successively higher ICs.

In Fig. 6.3(b), T is on the highest IC (IC₄), i.e., the straight line PQ has been a tangent to IC₄ at the point T. But as the consumer moves along the line PQ from the point T towards the point Q, he would be successively on lower ICs at the points V, W, etc.

In other words, the convex preference implies that the ICs are convex to the origin. However, they may have flat segment if the preference for the average is weak. It is generally assumed that well behaved preferences are convex because for the most part, goods are consumed together.

The consumer would want to trade some of one good for some of the other and end up consuming both, rather than specialising on only one of the two goods.