How a Consumer can Reach Equilibrium?

This article will guide you about how a consumer can reach equilibrium.

Given budget constraints and preferences, we now intend to demonstrate how a consumer can maximize his satisfaction or reach equilibrium. A consumer will be in equilibrium when he gets maximum satisfaction from the consumption of various commodities. One can show the point of satisfaction of the consumer with the aid of indifference curve and the budget line.

An indifference curve represents the combinations of two goods that yield the same level of satisfaction to the consumer. However, in attaining maximum satisfaction, a consumer is constrained by his (a) fixed and limited money income, and (b) the prices of the commodities that he buys.

We will explain the equilibrium of a consumer with the help of the indifference curve and the budget line. A budget line represents combinations of two goods that can be purchased if the entire money income is spent. Its slope is the price ratio, i.e.

P_X /P_Y

We are assuming that our consumer buys two goods X and Y, whose prices, P_X and P_Y, are given. He is confronted with his limited money income. He spends his income in purchasing X and Y in such a way that he gets the maximum amount of satisfaction.

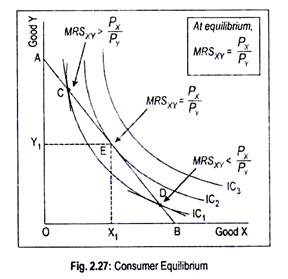
In Fig. 2.27, we measure the quantities of goods X and Y on the horizontal and vertical axes, respectively. AB is the initial budget line or consumption possibility line. The consumer, in fact, travels on the line AB. He cannot go beyond the budget line as his money income will not permit him to do so.

We have drawn a family of indifference curves, represented by IC₁, IC₂, and IC₃. A consumer will be in equilibrium when his budget line is tangential to the highest attainable indifference curve. In terms of Fig. 2.27, IC₁ crosses the budget line at points C and D. As IC₁ is a lower-order indifference curve, it must not represent highest satisfaction.

So the consumer will climb on to a new and higher indifference curve, IC₂. This new curve touches the budget line at point E. As IC₃ lies outside the budget line, the consumer cannot climb up to the higher indifference curve. In other words, this curve is not attainable. Therefore, point E is the equilibrium point where the consumer gets the maximum amount of satisfaction by purchasing OX₁ of X and OY₁ of Y.

Alternatively, a consumer will be in equilibrium when:

(i) the slope of the indifference curve becomes equal to the slope of the budget line (known as necessary condition, or mathematically, first-order condition)

(ii) the indifference curve is convex to the origin at the point of tangency (known as sufficient condition or second-order condition).

The slope of the indifference curve is the marginal rate of substitution between X and Y. Symbolically, it is MRS_XY. Again, the slope of the budget line is nothing but the price ratio of the two commodities.

Symbolically, it is P_X/P_Y.

Our consumer is in equilibrium at point E since MRS_XY = P_X/P_Y.

At points C and D, the slopes of the two curves are unequal.

At point C, MRS_XY > P_X/P_Y. The consumer will now travel’ along the budget line from point C toward E. This means that the consumer is willing to sacrifice Y more to have larger quantities of X. As he does this, his satisfaction increases without spending additional money. In the process, he reaches point E on IC₂ and gets maximum satisfaction.

The opposite is true at point D where MRS_XY > P_X/P_Y. So the consumer, in order to get higher satisfaction, will go on purchasing more of Y and less of X, of course, without incurring additional expenses.

Anyway, the optimum point is reached at E where the indifference curve is tangential to the budget line.

Thus, points C and D cannot be equilibrium points. Point E is the equilibrium point as

MRS_XY = P_X/P_Y.

So the necessary condition for equilibrium is fulfilled. Sufficient condition requires that the indifference curve must be convex to the origin at the point of tangency. Since these two conditions are fulfilled at point E, the consumer is in equilibrium at that point. This is called ‘interior solution’ where a consumer buys both the goods.