The below mentioned article provides an overview on the Principle of Marginal Rate of Technical Substitution (MRTS).
The principle of marginal rate of technical substitution (MRTS or MRS) is based on the production function where two factors can be substituted in variable proportions in such a way as to produce a constant level of output.
Salvatore defines MRTS thus :
“The marginal rate of technical substitution is the amount of an output that a firm can give up by increasing the amount of the other input by one unit and still remain on the same isoquant.”
ADVERTISEMENTS:
The marginal rate of technical substitution between two factors С (capital) and L (labour) MRTS is the rate at which L can be substituted for С in the production of good X without changing the quantity of output. As we move along an isoquant downward to the right, each point on it represents the substitution of labour for capital.
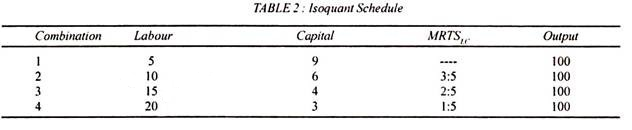
MRTS is the loss of certain units of capital which will just be compensated for by additional units of labour at that point. In other words, the marginal rate of technical substitution of labour for capital is the slope or gradient of the isoquant at a point. Accordingly, slope = MRTS, LC = – ∆С/∆ L. This can be understood with the aid of the isoquant schedule, in Table 2
The above table shows that in the second combination to keep to output constant at 100 units, the reduction of 3 units of capital requires the addition of 5 units of labour, MRTSLC = 3:5. In the third combination, the loss of 2 units of capital is compensated for by 5 more units of labour, and so on.
ADVERTISEMENTS:
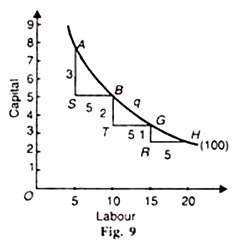
In Figure 9 at point B, the marginal rate of technical substitution is AS/SB, at point Q it is BT/TG and at H, it is GR/RH.
The isoquant AH reveals that as the units of labour are successively increased into the factor-combination to produce 100 units of good X, the reduction in the units of capital becomes smaller and smaller. It means that the marginal rate of technical substitution is diminishing.
This concept of the diminishing marginal rate of technical substitution (DMRTS) is parallel to the principle of diminishing marginal rate of substitution in the indifference curve technique.
ADVERTISEMENTS:
This tendency of diminishing marginal substitutability of factors is apparent from Table 2 and Figure 9. The MRTSLC continues to decline from 3:5 to 1:5 whereas in the Figure 9 the vertical lines below the triangles on the isoquant become smaller and smaller as we move downward so that GR < ВТ < AS. Thus, the marginal rate of technical substitution diminishes as labour is substituted for capital. It means that the isoquant must be convex to the origin at every point.