The broad class of monotonic increasing functions of homogeneous production functions, which includes also the underlying homogeneous functions, is called homothetic. If the production function is homogeneous (of any degree), the firm’s isoclines including long-run expansion path would be straight lines from the origin.
The homothetic production function has the same isoquants as those of its underlying homogeneous function, although, generally, with different quantity indexes.
That is why the firm’s expansion path and its isoclines would be straight lines from the origin also for a homothetic production function, and along any such straight line with a fixed ratio of the inputs, the firm’s MRTS of L for K or the ratio of MPL to MPK would be constant.
This is because for the underlying homogeneous function as also for the monotonic transformations of that function, the MRTS is a function of the ratio of the input quantities. In other words, the ratio of MPL to MPK would depend not upon absolute, but upon relative, input quantities.
ADVERTISEMENTS:
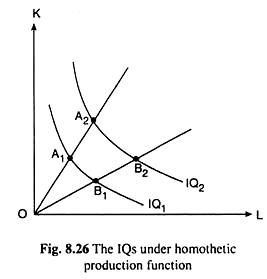
Therefore, in Fig. 8.26, the homothetic production function would give us
Slope of IQ1 at A1 = Slope of IQ2 at A2 and
Slope of IQ1 at B1 = Slope of IQ2 at B2.
where A1, A2 and B1, B2 are points on two different rays from the origin. That is, the slope of the IQs along any particular straight line from the origin would be a constant. Now, if the slopes of IQs are equal along any ray, then, at any point in the input space, MPL/MPK must not change with a proportionate change in L and K.
ADVERTISEMENTS:
Looking from the other side, since the input price ratio is constant, the iso-cost lines (ICLs) for different cost levels are parallel. Therefore, at the points of tangency between the ICLs and IQs, the slope of the IQs or the MRTS or MPL/MPK would be a constant, being equal to the slope of the ICLs.
This implies that if the production function is to be homothetic, then the ratio of the input quantities would be a constant at the points of tangency, i.e., the points of tangency lie on a ray from the origin. In other words, homotheticity requires that the firm’s expansion path coincides with such a ray.
A homogeneous production function is also homothetic—rather, it is a special case of homothetic production functions. In Fig. 8.26, the production function is homogeneous if, in addition, we have f(tL, tK) = tnQ where t is any positive real number, and n is the degree of homogeneity.
It follows from above that any homogeneous function is a homothetic function, but any homothetic function is not a homogeneous function. For example, Q = f (L, K) = a —(1/LαK) is a homothetic function for it gives us fL/fK = αK/L = constant. But it is not a homogeneous function for it does not give us f (tL, tK) = tnQ.