The technical rate of substitution in two dimensional cases is just the slope of the iso-quant. The firm has to adjust x2 to keep out constant level of output. If x1 changes by a small amount then x2 need to keep constant. In n dimensional case, the technical rate of substitution is the slope of an iso-quant surface. It is measured in a particular direction. Let assume that x2(x1) be the implicit function. It tells us how much of x2 takes to produce y. If we use X1 units then the effect will be different. By definition the function x2(x1) has to satisfy the identity.
If we take a derivative of the above function then we can express it as ∂ x 2(x*1)/∂x1.
If we differentiate the above equation then:
Or
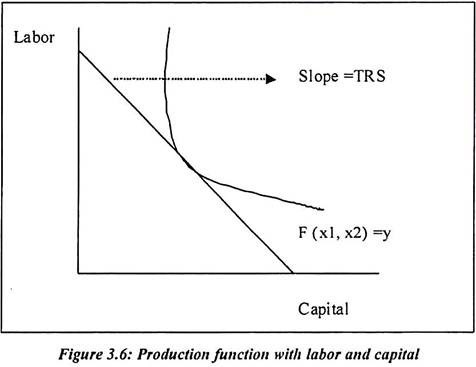
The above equation gives us the technical rate of substitution. There is another way of derive the technical rate of substitution. In the following figure 3.6, we can derive it. Technical rate of substitution measures the change in one input. Such change gets adjust in or to keep output constant. There are number of firms which are doing such practices. They also adjust another input in production. Sometimes, firms only hire labor for production. But strikes, labor union and labor disputes force firms to use technology in production function.
Therefore firms employ more capital and machinery as a factor of production. It is interesting to understand how the firms substitute labor for capital. Technology change among capital equipment suppliers lower the costs over time of the firm’s increasing delivery speed, using more flexible manufacturing methods, reducing the probability of defects, reducing costs of redesign and controlling production costs. While changing such composition some firms always keeps the output constant.
ADVERTISEMENTS:
It is shown as follows:
It can be presented in terms of derivative of two factors of production:
After solving above equation, we get following identity:
The above equation shows the implicit function. The total differential method may be used to calculate technical rate of substitution. The first method of calculation is wide and rigorous. But the second method is self-generated. But both methods are complete in their nature and both are useful.
Technical Rate of Substitution for Cobb-Douglas Technology:
In technical rate of substitution in Cobb-Douglas technology, we need to derive the technical rate of substitution. Suppose the given function is defined as f(x1, x2) = x1a x21-a,
It is further explained as follows:
Revised Technical Rate of Substitution:
ADVERTISEMENTS:
If we assume that technology is constant then a firm produces output with the help of inputs. The production function can be written as
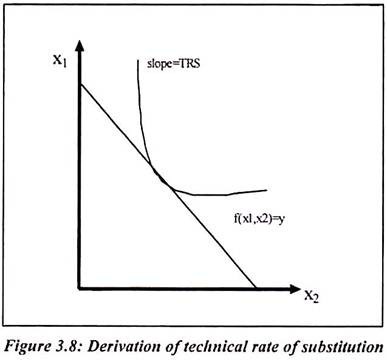
Such production function is constant and for particular time. Suppose we want to increase the amount of input that is capital and decrease the amount of input labor. The output is maintained at a constant level. It is determined by the TRS. In two dimensional cases, TRS is nothing but the slope of ISO quant. It is interesting to understand how one can adjust x2 to keep output constant while decreasing X1. Such change is shown in figure 3.8.
ADVERTISEMENTS:
In figure 3.8, we have derived technical rate of substitution. It shows a small change in vector of inputs. We can write it as
The associated change in the output is approximated by:
ADVERTISEMENTS:
The above equation is known as total differentiation of function f(x). Now we consider dx1 and dx2. It adjusts along with iso-quant and the output remains constant. The function can be derived as
The above equation is a slope of the iso-quant.
The TRS for Cobb -Douglas technology can be derived as follows:
Given that f(x1, x2) = x1ax21-a we can take derivative of the above function
ADVERTISEMENTS:
Above equation follows that: